Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Saffren, M. M.
and
Ng, E. W.
1971.
Recursive Algorithms for the Summation of Certain Series.
SIAM Journal on Mathematical Analysis,
Vol. 2,
Issue. 1,
p.
31.
Basu, N. K.
1973.
On Double Chebyshev Series Approximation.
SIAM Journal on Numerical Analysis,
Vol. 10,
Issue. 3,
p.
496.
Gautschi, Walter
1975.
Theory and Application of Special Functions.
p.
1.
1975.
Mathematical Functions and their Approximations.
p.
517.
Deufihard, P.
1976.
On algorithms for the summation of certain special functions.
Computing,
Vol. 17,
Issue. 1,
p.
37.
Marshall, Simon L
1998.
Convergence acceleration of Fourier series by analytical and numerical application of Poisson's formula.
Journal of Physics A: Mathematical and General,
Vol. 31,
Issue. 11,
p.
2691.
Barrio, R.
2001.
Stability of parallel algorithms to evaluate Chebyshev series.
Computers & Mathematics with Applications,
Vol. 41,
Issue. 10-11,
p.
1365.
Barrio, Roberto
2002.
Rounding error bounds for the Clenshaw and Forsythe algorithms for the evaluation of orthogonal polynomial series.
Journal of Computational and Applied Mathematics,
Vol. 138,
Issue. 2,
p.
185.
Jiang, Hao
Barrio, Roberto
Li, Housen
Liao, Xiangke
Cheng, Lizhi
and
Su, Fang
2011.
Accurate evaluation of a polynomial in Chebyshev form.
Applied Mathematics and Computation,
Vol. 217,
Issue. 23,
p.
9702.
Barrio, Roberto
Jiang, Hao
and
Serrano, Sergio
2013.
A General Condition Number for Polynomials.
SIAM Journal on Numerical Analysis,
Vol. 51,
Issue. 2,
p.
1280.
Smoktunowicz, Alicja
Smoktunowicz, Agata
and
Pawelec, Ewa
2015.
The three-term recursion for Chebyshev polynomials is mixed forward-backward stable.
Numerical Algorithms,
Vol. 69,
Issue. 4,
p.
785.
Gemignani, L.
2016.
Accurate polynomial root-finding methods for symmetric tridiagonal matrix eigenproblems.
Computers & Mathematics with Applications,
Vol. 72,
Issue. 4,
p.
992.
Hrycak, Tomasz
and
Schmutzhard, Sebastian
2018.
Evaluation of Chebyshev polynomials by a three-term recurrence in floating-point arithmetic.
BIT Numerical Mathematics,
Vol. 58,
Issue. 2,
p.
317.
Ledoux, Viviane
and
Moroz, Guillaume
2020.
Mathematical Aspects of Computer and Information Sciences.
Vol. 11989,
Issue. ,
p.
35.
Hrycak, Tomasz
and
Schmutzhard, Sebastian
2020.
Evaluation of Legendre polynomials by a three-term recurrence in floating-point arithmetic.
IMA Journal of Numerical Analysis,
Vol. 40,
Issue. 1,
p.
587.
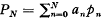 , where the coefficients an are assumed known, and the quantities pn, satisfy a linear three term recurrence relation, has been given by Clenshaw [1]. If we suppose that the pn satisfy the recurrence relation
, where the coefficients an are assumed known, and the quantities pn, satisfy a linear three term recurrence relation, has been given by Clenshaw [1]. If we suppose that the pn satisfy the recurrence relation 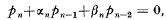 where αn and βn are, in general, functions of n, then PN may be found by constructing a sequence {bn} for n = N(−1)0, where the b satisfy the inhomogeneous recurrence relation
where αn and βn are, in general, functions of n, then PN may be found by constructing a sequence {bn} for n = N(−1)0, where the b satisfy the inhomogeneous recurrence relation 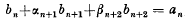 with the conditions,
with the conditions, 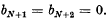 The sum PN is then given by
The sum PN is then given by  This result can be readily verified by multiplying each side of equation (1.2) by pn, summing from n = 0 to N, and making use of equations (1.1) and (1.3).
This result can be readily verified by multiplying each side of equation (1.2) by pn, summing from n = 0 to N, and making use of equations (1.1) and (1.3).

