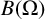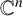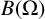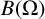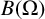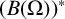EVALUATION FUNCTIONS AND REFLEXIVITY OF BANACH SPACES OF HOLOMORPHIC FUNCTIONS

Abstract

Let $B(\Omega )$ be a Banach space of holomorphic functions on a bounded connected domain $\Omega $ in ${{\mathbb C}^n}$. In this paper, we establish a criterion for $B(\Omega )$ to be reflexive via evaluation functions on $B(\Omega )$, that is, $B(\Omega )$ is reflexive if and only if the evaluation functions span the dual space $(B(\Omega ))^{*} $.

1 Introduction

Let $B(\Omega )$ be a Banach space of holomorphic functions on a bounded connected domain $\Omega $ in ${{\mathbb C}^n}$ . When $ n>1$ , we may assume that $\Omega $ is simply connected since any holomorphic function on $\Omega $ can be analytically extended to the holes in $\Omega $ by Hartog’s theorem. Let $K_{w}$ denote the evaluation function at $z\in \Omega $ , that is,

$$ \begin{align*} K_{z}(f)=f(z)\quad\text{for all } f\in B(\Omega). \end{align*} $$

The aim of this paper is to build a criterion for reflexivity of the Banach space $B(\Omega )$ via the evaluation functions on $B(\Omega ).$

Characterization of reflexivity of different types of Banach spaces is a fundamental problem in functional analysis. A very famous general criterion is the well-known Kakutani theorem, which uses the closed unit ball of the Banach space.

Turning to the specific Banach space $B(\Omega )$ on which we focus in this paper, finding a specific criterion for reflexivity is certainly an important problem.

Our idea is to use evaluation functions on $B(\Omega )$ , which play the role of reproducing kernels on a Hilbert space. However, when compared to reproducing kernels (on a Hilbert space), the properties of evaluation functions on Banach spaces are far less known.

To further understand the properties of evaluation functions on $B(\Omega )$ , we recall that in a reproducing kernel Hilbert space of holomorphic functions, the reproducing kernel has the very important property that $\{K_ {z} \mid z \in U\}$ spans the full space for any open subset or dense subset U of the domain (see for example, [2]). A similar conclusion may not hold in the general Banach space of holomorphic functions. Instead, we consider the following question related to the reflexivity of the specific Banach space $B(\Omega )$ .

Question 1.1. Can we characterize the reflexivity of $B(\Omega )$ via evaluation functions on $B(\Omega )$ ?

Recall again that $B(\Omega )$ is the Banach space of holomorphic functions on a bounded connected domain $\Omega $ in ${{\mathbb C}^n}$ . We list the following assumption about $\Omega $ and $B(\Omega )$ that is used in stating our main result.

1. (a) For each $z\in \Omega $ and for every $f\in B(\Omega )$ , the evaluation map $K_z: f\mapsto f(z)$ is a bounded linear functional on $B(\Omega )$ .

We now state our main result as follows, which answers the Question above.

Theorem 1.2. Let $\Omega $ and $B(\Omega )$ satisfy assumption (a). Then $B(\Omega )$ is reflexive if and only if for every arbitrary open subset or dense subset U of $\Omega , $

$$ \begin{align*} \bigvee_{z\in U}\{K_{z}\}=(B(\Omega ))^{*}, \end{align*} $$

where $\bigvee _{z\in U}\{K_{z}\}$ denotes the space spanned by $\{K_{z}\}_{z\in U}$ .

We note that the criterion established in Theorem 1.2 can be applied to various settings. For example, taking $\Omega $ to be the unit disk $\mathbb {D}$ in $\mathbb {C}$ , we see that our criterion applies to the Hardy spaces, Bergman spaces, Dirichlet spaces, Hardy–Sobolev spaces, and Bloch spaces on $\mathbb {D}$ .

2 Properties of evaluation functions on $B(\Omega)$

In this section, we discuss some properties of evaluation functions. It can be proved that the closed unit ball of the Banach space of analytic functions is a normal family by using the properties of evaluation functions. This conclusion is somewhat unexpected since, in general, the closed unit ball of an infinite dimensional Banach space is not weakly compact, which varies from the Hilbert space case. In fact, Kakutani’s theorem, also called the Eberlein–Shmuleyan theorem, showed that a necessary and sufficient condition for the closed unit ball of a Banach space to be weakly compact is that the space is reflexive (see [1]).

We begin by recalling a basic result in [6, page 5], followed by several auxiliary lemmas.

Lemma 2.1. If $\Lambda $ is a uniformly bounded family of holomorphic functions in $\Omega $ , then $\Lambda $ is equicontinuous on every compact subset of $\Omega .$ In other words, $\Lambda $ is a normal family.

Lemma 2.2. Suppose $\Omega $ and $B(\Omega )$ satisfy assumption (a), and $\mathcal {K}$ is an arbitrary compact subset of $\Omega .$ Then,

$$ \begin{align*} \sup_{z\in \mathcal{K}}\|K_{z}\|<\infty. \end{align*} $$

Proof. For any $f\in B(\Omega ),$ it is clear that

$$ \begin{align*} \sup_{z\in \mathcal{K}}|K_{z}(f)|=\sup_{z\in \mathcal{K}}|f(z)|<\infty \end{align*} $$

since f is holomorphic on $\Omega .$ By the uniform boundedness principle,

$$ \begin{align*} \sup_{z\in \mathcal{K}}\|K_{z}\|<\infty. \end{align*} $$

The proof is complete.

Lemma 2.3. Let $\Omega $ and $B(\Omega )$ satisfy assumption (a). Then, for an arbitrary sequence $\{f_{k}\}$ in $(B(\Omega ))_{1},$ the unit ball in $B(\Omega )$ , we obtain that $ \{f_{k}\}$ is a normal family.

Proof. Let $\mathcal {K}$ be an arbitrary compact subset of $\Omega .$ Choose another compact subset $\widetilde {\mathcal {K}}\subset \Omega $ and an open subset $\widetilde \Omega \subset \Omega $ such that

$$ \begin{align*} \mathcal{K}\subset \widetilde \Omega\subset \widetilde{\mathcal{K}}, \end{align*} $$

then

$$ \begin{align*} \sup_{k}\sup_{z\in \widetilde{\mathcal{K}}}|f_{k}(z)|&=\sup_{k}\sup_{z\in \widetilde{\mathcal{K}}}|K_{z}(f_{k})|\\ &\leq \sup_{k}\|f_{k}\|\cdot \sup_{z\in \widetilde{\mathcal{K}}}\|K_{z}\| \\ &\leq \sup_{z\in \widetilde{\mathcal{K}}}\|K_{z}\|<\infty \end{align*} $$

by Lemma 2.2. Thus,

$$ \begin{align*} \sup_{k}\sup_{z\in \widetilde \Omega}|f_{k}(z)|<\infty. \end{align*} $$

This implies that $\{f_{k}\}$ is uniformly bounded on $ \widetilde \Omega $ and also equicontinuous on every compact subset of $\widetilde \Omega $ by Lemma 2.1. In particular, $\{f_{k}\}$ is equicontinuous on $\mathcal {K}.$ This completes the proof.

It is well known that for $1<p<\infty ,$ a sequence $\{f_{k}\}$ in Bergman space $A^{p}(\mathbb {D})$ converges weakly to zero if and only if $\{\|f_{k}\|\}_{k}$ is bounded, and $f_{k}(z)\rightarrow 0$ uniformly on compact subsets of $\mathbb {D}$ as $k\rightarrow \infty $ (see [3, Exercise 1.6.1]). Since $A^{p}(\mathbb {D}) (1<p<\infty )$ is reflexive, we see that this conclusion is the consequence of Kakutani’s theorem and our Lemma 2.3.

Proposition 2.4. Suppose $\Omega $ and $B(\Omega )$ satisfy assumption (a), and U is an open subset or a dense subset of $\Omega $ . If $B(\Omega )$ is reflexive, then

$$ \begin{align*} \bigvee_{z\in U}\{K_{z}\}=(B(\Omega))^{*}. \end{align*} $$

Proof. Write $M=\bigvee _{z\in U}\{K_{z}\}.$ If $M\neq (B(\Omega ))^{*},$ then there is a nonzero $F\in (B(\Omega ))^{**}$ such that $F|_M=0.$ Here, $(B(\Omega ))^{**}$ is the second dual space of $B(\Omega ).$ Since $B(\Omega )$ is reflexive, there is a nonzero function $f\in B(\Omega )$ that satisfies $F=f^{**}\in (B(\Omega ))^{**},$ and thus

$$ \begin{align*} f(z)=K_{z}(f)=F(K_{z})=0. \end{align*} $$

This implies that $f=0.$ Thus, $F=f^{**}=0,$ which contradicts $F\neq 0.$ This contradiction completes the proof.

Let $ \mathfrak {B}$ be the Bloch space consisting of functions f with

$$ \begin{align*} \sup_{z\in {\mathbb D}}(1-|z|^2)|f'(z)|<\infty , \end{align*} $$

and the little Bloch space of ${\mathbb D},$ denoted by $\mathfrak {B}_{0}$ , be the closed subspace of $ \mathfrak {B}$ consisting of functions f with

$$ \begin{align*} \lim_{|z|\rightarrow 1^{-}}(1-|z|^2)f'(z)=0. \end{align*} $$

The following lemmas are well known.

Lemma 2.5 [8, Corollary 5.10].

$\mathfrak {B}_{0}$ is the closure in $ \mathfrak {B}$ of the set of polynomials. In particular, $\mathfrak {B}_{0}$ is separable.

Suppose $L^{1}_{a }(dA_{\alpha })$ is the weighted Bergman space with $dA_{\alpha }=c_{\alpha }(1-|z|^{2})^{\alpha }\,dA$ , a positive Borel measure on ${\mathbb D}$ , where $c_{\alpha }=\alpha +1$ for $\alpha>-1$ and $c_{\alpha }=1$ for $\alpha \leq -1$ (see [8, page 72]). Then we have the following lemma.

Lemma 2.6 [8, Theorem 5.15].

For any $\alpha> -1$ , we have $(\mathfrak {B}_{0})^{*}=L^{1}_{a }(dA_{\alpha })$ under the integral pairing

$$ \begin{align*} \langle f,g \rangle_{\alpha}=\int_{{\mathbb D}} f(z)\overline{g(z)}\,dA_{\alpha}(z). \end{align*} $$

Here, $ \mathfrak {B}_{0}$ is equipped with the norm $\|f\| = |f(0)| + \|f\|_{ \mathfrak {B}_{0}}.$

It is clear that $L^{1}_{a }(dA_{0})=A^{1}({\mathbb D}),$ the classical Bergman space.

In general, if $B(\Omega )$ is not reflexive, then the set of evaluation functions may not span the dual space of $B(\Omega ).$ For example, it is well known that $A^{1}(\mathbb {D}),$ the Bergman space on $\mathbb {D},$ is not reflexive; its dual space is the Bloch space $\mathfrak {B}$ (see [3]). The following proposition verifies our conclusion.

Proposition 2.7. Suppose $A^{1}(\mathbb {D})$ is the Bergman space on the unit disc $\mathbb {D}$ in the complex plane $\mathbb {C}.$ Then for any $z\in \mathbb {D} ,$ the evaluation function $K_{z}$ is bounded on $A^{1}(\mathbb {D}),$ and

$$ \begin{align*} \bigvee_{z\in \mathbb{D} }\{K_{z}\}= \mathfrak{B}_{0}\subsetneqq \mathfrak{B}. \end{align*} $$

Proof. It is obvious that $K_{z}$ is bounded for any $z\in \mathbb {D}.$ We prove that

$$ \begin{align*} \bigvee_{z\in \mathbb{D} }\{K_{z}\}= \mathfrak{B}_0, \end{align*} $$

and further, $ \bigvee _{z\in \mathbb {D} }\{K_{z}\}\subsetneqq \mathfrak {B}. $

It is clear that for any $z\in {\mathbb D}, K_{z}\in \mathfrak {B}_0.$ Hence, $ \bigvee _{z\in \mathbb {D} }\{K_{z}\}\subset \mathfrak {B}_0. $ If $ \bigvee _{z\in \mathbb {D} }\{K_{z}\}\neq \mathfrak {B}_0, $ then there is a nonzero $F\in (\mathfrak {B}_0)^{*}$ such that $F|_{\bigvee _{z\in \mathbb {D} }\{K_{z}\}}=0.$ By Lemma 2.6, there is an $f\in L^{1}_{a }(dA_{\alpha })$ such that

$$ \begin{align*} F(g)=\int_{{\mathbb D}}g\overline{f}\,dA_{\alpha }. \end{align*} $$

In particular, for any $z\in {\mathbb D},$

$$ \begin{align*} F(K_{z})=\int_{{\mathbb D}}K_{z}\overline{f}\,dA_{\alpha }=0. \end{align*} $$

This shows that $f(z)=0$ for any $z\in D,$ and hence $f=0.$ Consequently, $F=0.$ This contradiction completes the proof.

Proposition 2.8. Let $\Omega $ and $B(\Omega )$ satisfy assumption (a). If $\{z_{k}\}\subset \Omega $ is a sequence that convergences to $w\in \Omega ,$ then

$$ \begin{align*} \|K_{z_{k}}-K_{w}\|\rightarrow 0. \end{align*} $$

Proof. Assuming the contrary, then there is an $\epsilon _{0}>0$ and a sequence $\{f_{k}\}\subset (B(\Omega ))_{1}$ , the unit ball of $B(\Omega ),$ such that

$$ \begin{align*} |(K_{z_{k}}-K_{w})(f_{k})|\geq \epsilon_{0}. \end{align*} $$

That is,

$$ \begin{align*} |f_{k}(z_{k})-f_{k}(w)|\geq \epsilon_{0}. \end{align*} $$

Write $F_{k}=f_{k}^{**}\in [(B(\Omega ))^{**}]_{1},$ where $(B(\Omega ))^{**}$ is the second dual space of $B(\Omega ), [(B(\Omega ))^{**}]_{1}$ is the unit ball of $(B(\Omega ))^{**}.$ Then there is a subsequence $\{F_{k_{j}}\}$ such that $F_{k_{j}}$ converges in the weak-star topology to $F_{0}\in (B(\Omega ))^{**}.$ In particular,

$$ \begin{align*} F_{k_{j}}(K_{z})\rightarrow F_{0}(K_{z}) \quad \mathrm{as\ } j\to\infty. \end{align*} $$

However,

$$ \begin{align*} F_{k_{j}}(K_{z})=K_{z}(f_{k_{j}})=f_{k_{j}}(z), \end{align*} $$

and hence there is a holomorphic function f on $\Omega $ such that

$$ \begin{align*} f_{k_{j}}(z)\rightarrow f(z)=F_{0}(K_{z})\quad \mathrm{as\ } j\to\infty. \end{align*} $$

Assume $\mathcal {K}\subset \Omega $ is any compact subset of $\Omega ,$ then

$$ \begin{align*} \sup_{k_{j}}\sup_{z\in \mathcal{K}}|f_{k_{j}}(z)|\leq \sup_{k_{j}}\|f_{k_{j}}\|\cdot \sup_{z\in \mathcal{K}}\|K_{z}\| \leq\sup_{z\in \mathcal{K}}\|K_{z}\| <\infty. \end{align*} $$

By Lemma 2.3, we know that $\{f_{k_{j}}\}$ is a normal family. Further,

$$ \begin{align*} f_{k_{j}}|_{\mathcal{K}}\rightarrow f|_{\mathcal{K}}\quad \text{uniformly as } j\rightarrow \infty. \end{align*} $$

This contradicts $|f_{k}(z_{k})-f_{k}(w)|\geq \epsilon _{0},$ which means $\|K_{z_{k}}-K_{w}\|\rightarrow 0 .$

According to an example of Manhas and Zhao in [4], it may happen in a reproducing kernel Hilbert space that as z tends to the boundary of $\Omega $ , the kernel functions satisfy $\|K_{z}\|\rightarrow \infty $ but the normalized reproducing kernels $k_{z}$ do not converge to 0 weakly. However, if the polynomials are dense in the space, this phenomenon does not occur.

Proposition 2.9. Let $\Omega $ and $B(\Omega )$ satisfy assumption (a), and $P[\Omega ]$ , the ring of polynomials on $\Omega ,$ is dense in $B(\Omega ).$ For any sequence $\{z_{k}\}\subset \Omega $ and $\zeta \in \partial \Omega ,$ if $\|K_{z_{k}}\|\rightarrow \infty $ as $z_{k}\rightarrow \zeta ,$ then

$$ \begin{align*} k_{z_{k}}=\frac{K_{z_{k}}}{\|K_{z_{k}}\|}\stackrel{weak^{*}}{\longrightarrow} 0 \quad\text{as } k\rightarrow \infty. \end{align*} $$

Proof. Assuming $P\in P[\Omega ],$ it is obvious that $K_{z_{k}}(P)\rightarrow P(\zeta )$ as $k\rightarrow \infty .$ Since $\|K_{z_{k}}\|\rightarrow ~\infty ,$

$$ \begin{align*} k_{z_{k}}(P)=\frac{K_{z_{k}}}{\|K_{z_{k}}\|}(P)=\frac{P(z_{k})}{\|K_{z_{k}}\|}\rightarrow 0 \quad\text{as } k\to\infty. \end{align*} $$

For any $f\in B(\Omega ),$ take a sequence $\{P_{m}\}\subset P[\Omega ]$ such that $\|P_{m}-f\|\rightarrow 0$ as $m\rightarrow \infty .$ Then,

$$ \begin{align*} |k_{z_{k}}(f)|&=\bigg|\frac{K_{z_{k}}}{\|K_{z_{k}}\|}(f)\bigg|\\ &\leq \bigg|\frac{K_{z_{k}}}{\|K_{z_{k}}\|}(f)-\frac{K_{z_{k}}}{\|K_{z_{k}}\|}(P_{m})\bigg| +\bigg|\frac{K_{z_{k}}}{\|K_{z_{k}}\|}(P_{m})\bigg|\\ &\leq \bigg\|\frac{K_{z_{k}}}{\|K_{z_{k}}\|}\bigg\|\cdot \|f-P_{m}\|+\bigg|\frac{K_{z_{k}}}{\|K_{z_{k}}\|}(P_{m})\bigg|\\ &= \|f-P_{m}\|+\bigg|\frac{K_{z_{k}}}{\|K_{z_{k}}\|}(P_{m})\bigg|. \end{align*} $$

This shows that $k_{z_{k}}(f)\rightarrow 0.$ That is,

$$ \begin{align*} k_{z_{k}}=\frac{K_{z_{k}}}{\|K_{z_{k}}\|}\stackrel{\text{weak}^{*}}{\longrightarrow} 0 \quad\text{as } k\rightarrow \infty. \end{align*} $$

The proof is complete.

It should be noted that, similar to the reproducing kernel of the Hilbert space of analytic functions, the boundary behavior of the evaluation function on the Banach space of analytic functions depends on the structure of the space. For example, as we know, for $1\leq p<\infty ,$ if $\beta>n/p, $ then $\|K_{z}\|$ , the norm of the evaluation function $K_{z}$ on Hardy–Sobolev space $H_{\beta }^{p}$ (see [5]), is bounded on $ \mathbb {B}_{n} .$ As any function in $H_{\beta }^{p} (\mathbb {B}_{n})$ is continuous on the boundary of $\mathbb {B}_{n},$ it can be seen that when the sequence $\{z_{k}\}$ in $\mathbb {B}_{n} $ converges to a point $\zeta \in \partial \mathbb {B}_{n},$ then according to the norm in $H_{\beta }^{p} (\mathbb {B}_{n}), K_{z_{k}}$ converges to $K_{\zeta },$ the evaluation function at $\zeta .$ Thus,

$$ \begin{align*} \|k_{z_{k}}-k_{\zeta }\|\rightarrow 0 \quad\text{as } k\rightarrow \infty , \end{align*} $$

where $k_{z_{k}}= {K_{z_{k}}}/{\|K_{z_{k}}\|}, k_{\zeta } = {K_{\zeta }}/{\|K_{\zeta }\|}.$ If $\beta \leq n/p, $ then $\|K_{z}\|\rightarrow \infty $ as $z\rightarrow \partial \mathbb {B}_{n}$ and

$$ \begin{align*} k_{z}=\frac{K_{z}}{\|K_{z}\|}\stackrel{\text{weak}^{*}}{\longrightarrow} 0 \quad\text{as } z\rightarrow \partial \mathbb{B}_{n}. \end{align*} $$

3 Proof of Theorem 1.2

Proof. We need only to prove the sufficiency by Proposition 2.4. Assume

$$ \begin{align*} \bigvee_{z\in \Omega}\{K_{z}\}=(B(\Omega))^{*}. \end{align*} $$

We prove that $(B(\Omega ))_{1}$ is weakly compact, and further $B(\Omega )$ is reflexive by Kakutani’s theorem. Assume $\{f_{k}\}\subset (B(\Omega ))_{1}.$ By Lemma 2.3, there is a subsequence $\{f_{k_{j}}\}$ such that $f_{k_{j}}(z)\rightarrow f(z)$ uniformly on compact subsets of $\Omega ,$ where f is a holomorphic function on $\Omega .$ Thus, for any $z\in \Omega ,$

$$ \begin{align*} K_{z}(f_{k_{j}})=f_{k_{j}}(z)\rightarrow f(z). \end{align*} $$

This implies that $ \{K_{z}(f_{k_{j}})\}$ is convergent. Further, for any finite linear combination $\sum _{i=1}^{m}\alpha _{i}K_{z_{i}},$ $\{ \sum _{i=1}^{m}\alpha _{i}K_{z_{i}}(f_{k_{j}})\}$ is also convergent. Since

$$ \begin{align*} \bigvee_{z\in \Omega }\{K_{z}\}= (B(\Omega))^{*}, \end{align*} $$

we see that $\{F(f_{k_{j}})\}$ is convergent for any $F\in (B(\Omega ))^{*}.$ Since F is chosen arbitrarily, we know that there is a $G\in (B(\Omega ))^{**}$ such that $f_{k_{j}}^{**}(F)\rightarrow G(F)$ for any $F\in (B(\Omega ))^{*}$ since $ (B(\Omega ))^{**}$ is weak-star compact. Writing $f_{G}(z)=G(K_{z})$ for any $z\in \Omega ,$ we see that

$$ \begin{align*} f_{G}(z)=G(K_{z})=\lim_{j\rightarrow \infty }f_{k_{j}}^{**}(K_{z})=\lim_{j\rightarrow \infty }f_{k_{j}}(z)=f(z). \end{align*} $$

Hence, $f_{G}$ is a holomorphic function. For any $F\in (B(\Omega ))^{*}, F(f_{G})$ is well defined and $F(f_{k_{j}})\rightarrow F(f_{G}).$ By $ \bigvee _{z\in \Omega }\{K_{z}\}=(B(\Omega ))^{*}$ again, there exists a sequence $\{P_{m}\}\subset \bigvee _{z\in \Omega }\{K_{z}\}$ such that

$$ \begin{align*} P_{m}=\sum_{i=1}^{k_{m}}\alpha_{i}^{(m)}K_{z_{i}^{(m)}}\rightarrow F\quad\text{in } (B(\Omega))^{*} \text{ as } m\to\infty. \end{align*} $$

For arbitrary $\alpha \in \mathbb {C},$ since

$$ \begin{align*} F(\alpha f_{G})&=\lim_{m\rightarrow \infty }P_{m}(\alpha f_{G})\\ &=\alpha \lim_{m\rightarrow \infty }P_{m}( f_{G})\\ &=\alpha \lim_{m\rightarrow \infty }G(P_{m})\\ &=\alpha G(F)\\ &=\alpha F(f_{G}), \end{align*} $$

we see that $F(\alpha f_{G})=\lim \limits _{m\rightarrow \infty }P_{m}(\alpha f_{G})$ is well defined and $F(\alpha f_{G})=\alpha F(f_{G}).$ Define

$$ \begin{align*} \|f_{G}\|:=\sup_{F\in ((B(\Omega ))^{*})_{1}}|F(f_{G})|. \end{align*} $$

Noting that

$$ \begin{align*} \lim_{j\rightarrow \infty }F(f_{k_{j}})= F(f_{G}) \end{align*} $$

and

$$ \begin{align*} \|F(f_{k_{j}})\|\leq \|F\|\|f_{k_{j}}\|\leq 1, \end{align*} $$

we get that $\|f_{G}\|<\infty .$ We now prove $f_{G}\in B(\Omega )$ by contradiction. Suppose $f_{G}\notin B(\Omega ),$ then we define

$$ \begin{align*} B=\bigvee\{B(\Omega ), f_{G}\}, \end{align*} $$

the space spanned by $B(\Omega )$ and $f_{G}.$ That is,

$$ \begin{align*} B=\{f+\alpha f_{G}\mid f\in B(\Omega ),\alpha \in \mathbb{C}\}. \end{align*} $$

For any $g=f+\alpha f_{G},$ define the norm of g as

$$ \begin{align*} \|g\|_{1}=\|f\|+|\alpha |\| f_{G}\|. \end{align*} $$

Then $\|\cdot \|_{1}|_{B(\Omega )}=\|\cdot \|.$ It is easy to check that $B^{*}=(B(\Omega ))^{*}.$ In fact, for any ${F\in (B(\Omega ))^{*}, F}$ is well defined on B since $F( f_{G})$ is well defined, and

$$ \begin{align*} |F(f+\alpha f_{G})|=|F(f)+\alpha F(f_{G})|\leq \|F\|(\|f\|+|\alpha |\|f_{G}\|)=\|F\|\|f+\alpha f_{G}\|. \end{align*} $$

Hence, $F\in B^{*}.$ Conversely, if $F\in B^{*},$ then for any $f\in B(\Omega ), |F(f)|\leq \|F\|\|f\|_{1}=\|F\|\|f\|,$ this shows that $F\in (B(\Omega ))^{*}.$ By the assumption $f_{G}\notin B(\Omega ),$ there is an $F_{0}\in B^{*}$ such that $F_{0}|_{B(\Omega )}=0$ , and $F_{0}(f_{G})\neq 0.$ However, we know that the sequence ${\{f_{k_{j}}\}\subset B(\Omega )}$ such that $F(f_{k_{j}})\rightarrow F(f_{G})$ for any $F\in (B(\Omega ))^{*}.$ This implies that ${F_{0}(f_{G})=0}$ since $B^{*}=(B(\Omega ))^{*}.$ This contradiction shows that $f_{G}\in B(\Omega ).$ Thus, $G=f_{G}^{**}.$ This shows that $(B(\Omega ))_{1}$ is weakly compact, and then $ B(\Omega )$ must be reflexive by Kakutani’s theorem.

Now let U be any open subset or dense subset U of $\Omega .$ We are to prove that

$$ \begin{align*} \bigvee_{z\in U}\{K_{z}\}=(B(\Omega))^{*} \end{align*} $$

if and only if

$$ \begin{align*} \bigvee_{z\in \Omega}\{K_{z}\}=(B(\Omega))^{*}. \end{align*} $$

We prove this argument by contradiction. Assume that

$$ \begin{align*} \bigvee_{z\in \Omega}\{K_{z}\}=(B(\Omega))^{*} \end{align*} $$

and there is an open subset or dense subset U of $\Omega $ with

$$ \begin{align*} \bigvee_{z\in U}\{K_{z}\}\neq (B(\Omega))^{*}. \end{align*} $$

Then there is a nonzero $G\in (B(\Omega ))^{**}$ such that $G|_{ \bigvee _{z\in U}\{K_{z}\}}=0.$ Since $B(\Omega )$ is reflexive, there is a nonzero $g\in B(\Omega )$ such that $G=g^{**}.$ Thus, for any $z\in U,$

$$ \begin{align*} g(z)=g^{**}(K_{z})=G(K_{z})=0. \end{align*} $$

Further, $g=0$ on $\Omega $ by the uniqueness of the extension of holomorphic functions. The contradiction completes the proof.

Remark 3.1. It is well known that the dual space of $H ^ {1}(\mathbb {D})$ is BMOA, the holomorphic function space with bounded mean oscillation. According to Theorem 1.2, the evaluation functions on $H ^ {1}(\mathbb {D})$ cannot span BMOA since $H ^ {1}(\mathbb {D})$ is not reflexive. Some other classical holomorphic function spaces, such as the Dirichlet space $\mathfrak {D}^{1}(\mathbb {D})$ , the Hardy–Sobolev space $H_{\beta }^{1}(\mathbb {D}) (\beta \in \mathbb {R}),$ are also nonreflexive, so the evaluation functions on them cannot span their dual spaces.

4 Further discussion

As we know, an evaluation function need not be well defined even in the Hilbert space of holomorphic functions. For instance, let $H^{2}(\beta )$ be the weighted Hardy space with weight $\beta _{n}= {1}/{2^{n}}$ (see [7]). If we set $f(z)=\sum _{n=0}^{\infty }(\tfrac 43)^nz^{n},$ then

$$ \begin{align*} \|f\|=\sqrt{\sum_{n=0}^{\infty }\bigg(\frac{4}{3}\bigg)^{2n}\bigg(\frac{1}{2}\bigg)^{2n}} = \sqrt{\sum_{n=0}^{\infty}\bigg(\frac{2}{3}\bigg)^{2n}} < \infty. \end{align*} $$

However, $K_{z_{0}}(f)=\sum _{n=0}^{\infty }({16}/{15})^{n}=\infty $ for $z_0=\tfrac 45$ , a point in the unit disc ${\mathbb D}$ , which means that for some $z\in {\mathbb D}$ , $K_{z}$ is not well defined. This is why we have to make assumption (a).

An interesting phenomenon is that the evaluation functions may still span the whole dual space of the Banach space $B(\Omega )$ of analytic functions as long as the evaluation function is well defined and bounded on an open subset or dense subset of the domain $\Omega .$ In fact, we have the following theorem.

Theorem 4.1. Let $B(\Omega )$ be a Banach space of holomorphic functions on a bounded connected domain $\Omega $ in ${{\mathbb C}^n}$ . If there is an open subset or dense subset U of the domain $\Omega $ such that $K_{z}$ is bounded on $B(\Omega ),$ then $B(\Omega )$ is reflexive if and only if

$$ \begin{align*} \bigvee_{z\in U}\{K_{z}\}= (B(\Omega))^{*}. \end{align*} $$

Proof. The proof is similar to that of Theorem 1.2, but for convenience, we give the details here.

First, assume that $B(\Omega )$ is reflexive. Write $M=\bigvee _{z\in U}\{K_{z}\},$ and if $M\neq (B(\Omega ))^{*},$ then there is a nonzero $F\in (B(\Omega ))^{**}$ such that $F|_M=0.$ Here, $(B(\Omega ))^{**}$ is the second dual space of $B(\Omega ).$ Since $B(\Omega )$ is reflexive, there is a nonzero function $f\in B(\Omega )$ , which satisfies $F=f^{**}\in (B(\Omega ))^{**},$ and thus

$$ \begin{align*} f(z)=K_{z}(f)=F(K_{z})=0. \end{align*} $$

This implies that $f=0.$ Thus, $F=f^{**}=0,$ which contradicts $F\neq 0.$ This contradiction means that

$$ \begin{align*} \bigvee_{z\in U}\{K_{z}\}= (B(\Omega))^{*}. \end{align*} $$

Second, if

$$ \begin{align*} \bigvee_{z\in U}\{K_{z}\}= (B(\Omega))^{*}, \end{align*} $$

we prove that $(B(\Omega ))_{1}$ is weakly compact and further $B(\Omega )$ is reflexive by Kakutani’s theorem. Assume $\{f_{k}\}\subset (B(\Omega ))_{1}.$ By Lemma 2.3, there is a subsequence $\{f_{k_{j}}\}$ such that $f_{k_{j}}(z)\rightarrow f(z)$ uniformly on compact subsets of $\Omega ,$ where f is a holomorphic function on $\Omega .$ Thus, for any $z\in U ,$

$$ \begin{align*} K_{z}(f_{k_{j}})=f_{k_{j}}(z)\rightarrow f(z). \end{align*} $$

This implies that $ \{K_{z}(f_{k_{j}})\}$ is convergent. Further, for any finite linear combination $\sum _{i=1}^{m}\alpha _{i}K_{z_{i}},$ $\{ \sum _{i=1}^{m}\alpha _{i}K_{z_{i}}(f_{k_{j}})\}$ is also convergent. Since

$$ \begin{align*} \bigvee_{z\in U}\{K_{z}\}= (B(\Omega))^{*}, \end{align*} $$

we see that $\{F(f_{k_{j}})\}$ is convergent for any $F\in (B(\Omega ))^{*}.$ Since F is chosen arbitrarily, we know that there is a $G\in (B(\Omega ))^{**}$ such that $f_{k_{j}}^{**}(F)\rightarrow G(F)$ for any $F\in (B(\Omega ))^{*}$ as $ (B(\Omega ))^{**}$ is weak-star compact. Writing $f_{G}(z)=G(K_{z})$ for any $z\in U ,$

$$ \begin{align*} f_{G}(z)=G(K_{z})=\lim_{j\rightarrow \infty }f_{k_{j}}^{**}(K_{z})=\lim_{j\rightarrow \infty }f_{k_{j}}(z)=f(z). \end{align*} $$

Hence, $f_{G}$ is a holomorphic function on U, and f is the holomorphic extension of $f_{G}.$ Thus, for any $F\in (B(\Omega ))^{*}, F(f_{G})$ is well defined, and $F(f_{k_{j}})\rightarrow F(f_{G}).$ By $ {\bigvee _{z\in U}\{K_{z}\}=(B(\Omega ))^{*}}$ again, there exists a sequence $\{P_{m}\}\subset \bigvee _{z\in U}\{K_{z}\}$ such that

$$ \begin{align*} P_{m}=\sum_{i=1}^{k_{m}}\alpha_{i}^{(m)}K_{z_{i}^{(m)}}\rightarrow F \quad\text{in } (B(\Omega))^{*} \text{ as } m\to\infty. \end{align*} $$

For arbitrary $\alpha \in \mathbb {C},$ since

$$ \begin{align*} F(\alpha f_{G})&=\lim_{m\rightarrow \infty }P_{m}(\alpha f_{G})\\ &=\alpha \lim_{m\rightarrow \infty }P_{m}( f_{G})\\ &=\alpha \lim_{m\rightarrow \infty }G(P_{m})\\ &=\alpha G(F)\\ &=\alpha F(f_{G}), \end{align*} $$

we see that $F(\alpha f_{G})=\lim \limits _{m\rightarrow \infty }P_{m}(\alpha f_{G})$ is well defined, and $F(\alpha f_{G})=\alpha F(f_{G}).$ Define

$$ \begin{align*} \|f_{G}\|:=\sup_{F\in ((B(\Omega ))^{*})_{1}}|F(f_{G})|. \end{align*} $$

Note that

$$ \begin{align*} \lim_{j\rightarrow \infty }F(f_{k_{j}})= F(f_{G}) \end{align*} $$

and

$$ \begin{align*} \|F(f_{k_{j}})\|\leq \|F\|\|f_{k_{j}}\|\leq 1, \end{align*} $$

we get that $\|f_{G}\|<\infty .$ We now prove $f_{G}\in B(\Omega )$ by contradiction. Suppose $f_{G}\notin B(\Omega ),$ then we define

$$ \begin{align*} B=\bigvee\{B(\Omega ), f_{G}\}, \end{align*} $$

the space spanned by $B(\Omega )$ and $f_{G}.$ That is,

$$ \begin{align*} B=\{f+\alpha f_{G}\mid f\in B(\Omega ),\alpha \in \mathbb{C}\}. \end{align*} $$

For any $g=f+\alpha f_{G},$ define the norm of g as

$$ \begin{align*} \|g\|_{1}=\|f\|+|\alpha |\| f_{G}\|. \end{align*} $$

Then $\|\cdot \|_{1}|_{B(\Omega )}=\|\cdot \|.$ It is easy to check that $B^{*}=(B(\Omega ))^{*}.$ In fact, for any ${F\in (B(\Omega ))^{*}, F}$ is well defined on B since $F( f_{G})$ is well defined, and

$$ \begin{align*} |F(f+\alpha f_{G})|=|F(f)+\alpha F(f_{G})|\leq \|F\|(\|f\|+|\alpha |\|f_{G}\|)=\|F\|\|f+\alpha f_{G}\|. \end{align*} $$

Hence, $F\in B^{*}.$ Conversely, if $F\in B^{*},$ then for any $f\in B(\Omega ), |F(f)|\leq \|F\|\|f\|_{1}=\|F\|\|f\|,$ which shows that $F\in (B(\Omega ))^{*}.$ By the assumption $f_{G}\notin B(\Omega ),$ there is an ${F_{0}\in B^{*}}$ such that $F_{0}|_{B(\Omega )}=0$ and $F_{0}(f_{G})\neq 0.$ However, we know that there is a sequence $\{f_{k_{j}}\}\subset B(\Omega )$ such that $F(f_{k_{j}})\rightarrow F(f_{G})$ for any $F\in (B(\Omega ))^{*}.$ This implies that ${F_{0}(f_{G})=0}$ since $B^{*}=(B(\Omega ))^{*}.$ This contradiction shows that $f_{G}\in B(\Omega ).$ Thus, $G=f_{G}^{**}.$ This shows that $(B(\Omega ))_{1}$ is weakly compact and then $ B(\Omega )$ must be reflexive by Kakutani’s theorem. This completes the proof.

Remark 4.2. We know that $K_z$ is well defined on the weighted Hardy space $H^2(\beta )$ with weight $\beta _n= {1}/{2^n}$ for $z\in U=\{z\in {\mathbb D}||z|<\tfrac 12\}.$ Although the functions in $H^2(\beta )$ are not necessarily holomorphic on the entire unit disk, still

$$ \begin{align*} \bigvee_{z\in U}\{K_{z}\}= H^2(\beta). \end{align*} $$

In fact, if

$$ \begin{align*} \bigvee_{z\in U}\{K_{z}\}\neq H^2(\beta), \end{align*} $$

then there exists a nonzero $f\in H^2(\beta )$ such that

$$ \begin{align*} f\perp \bigvee_{z\in U}\{K_{z}\}. \end{align*} $$

Thus,

$$ \begin{align*} f(z)=K_z(f)=0\quad\text{for all } z\in U. \end{align*} $$

Further, $f=0.$ This contradiction shows that $ \bigvee _{z\in U}\{K_{z}\}= H^2(\beta ). $

However, there also exists a weighted Hardy space such that for any nonzero $z\in {\mathbb D}$ , $K_z$ cannot be well defined on it. For instance, let $H^2(\beta )$ be the weighted Hardy space with the weight $\beta _n= {1}/{n^n}.$ Then, for arbitrary $z\in {\mathbb D}-\{0\}, K_z$ cannot be well defined on $H^2(\beta ).$ Hence, Theorem 4.1 fails although $H^2(\beta )$ is a Hilbert space.

Remark 4.2 shows that a function in the weighted Hardy space $H^2(\beta )$ may not necessarily be a holomorphic function on the entire unit disk, and it may even be undefined on a disk without center, or a space composed only of a formal power series. When the weight $\beta =\{\beta _n\}_{n=0}^{\infty }$ satisfies some conditions, the space $H^2(\beta )$ is indeed composed of holomorphic functions on the disk.

Proposition 4.3. Assuming $H^2(\beta )$ is the weighted Hardy space with weight $\beta =\{\beta (n)\}$ , then $K_{z}$ is bounded for arbitrary $z\in {\mathbb D}$ if and only if

$$ \begin{align*}\lim_{n\rightarrow \infty}\sqrt[n]{\beta(n)}\geq1.\end{align*} $$

Proof. Assume for any $z\in {\mathbb D}$ , $K_{z}$ is bounded on $H^2_{\beta }({\mathbb D})$ . Let $e_{n}(z)= {z^{n}}/{\| z^{n}\|} = ({1}/{\beta (n)}) z^{n}$ , then $K_{z}(w)=\sum _{n=0}^{\infty }\overline {e_{n}(z)}e_{n}(w)$ (see [8]) and

$$ \begin{align*} \| K_{z}\|^2=\langle K_{z}, K_{z}\rangle=\sum_{n=0}^{\infty}|e_{n}(z)|^{2}=\sum_{n=0}^{\infty}\frac{1}{\beta^{2}(n)}|z^{n}|^{2}<+\infty,\end{align*} $$

and thus,

$$ \begin{align*} \lim_{n\rightarrow \infty}\frac{1}{\sqrt[n]{\beta^{2}(n)}}|z|^{2}\leq 1. \end{align*} $$

That is, $\lim _{n\rightarrow \infty }\sqrt [n]{\beta ^{2}(n)}\geq |z|^{2},$ which means $\lim _{n\rightarrow \infty } \sqrt [n]{\beta ^{2}(n)}\geq 1$ by the arbitrariness of z. Further, $\lim _{n\rightarrow \infty }\sqrt [n]{\beta (n)}\geq 1$ .

Conversely, assume $\lim _{n\rightarrow \infty }\sqrt [n]{\beta (n)}\geq 1$ , then $\lim _{n\rightarrow \infty } ({1}/{\sqrt [n]{\beta (n)}}) |z|<1$ for arbitrary $z\in {\mathbb D}$ . Hence,

$$ \begin{align*} \sum_{n=0}^{\infty }\frac{1}{\beta^{2}(n)}|z^n|^{2}<+\infty, \end{align*} $$

that is, $\|K_{z}\|^{2}<+\infty .$

The following proposition is almost obvious, but it tells us that the boundedness of the evaluation function on the Banach space of the holomorphic functions depends on some regularity of the functions in the space, that is, the convergence of the function sequence in the space means the pointwise convergence of this function sequence.

Proposition 4.4. Let $\Omega $ be a bounded domain in ${\mathbb C}^{n}$ , $B(\Omega )$ is the Banach space of holomorphic functions on $\Omega $ . Then for $z\in \Omega $ , the evaluation function $K_{z}$ is bounded on $B(\Omega )$ if and only if for arbitrary $f_{n}$ , f in $B(\Omega )$ with $\| f_{n}-f\|\rightarrow 0$ ,

$$ \begin{align*}f_{n}(z)\rightarrow f(z).\end{align*} $$

Proof. Since for any $f\in B(\Omega ), f$ is holomorphic on $\Omega ,$ we see that $|f(z)|<\infty ,$ which means that $K_{z}$ is well defined for arbitrary $z\in \Omega .$ If $K_{z}$ is bounded, then it is clear that $f_{n}(z)\rightarrow f(z)$ if $\| f_{n}-f\|\rightarrow 0$ .

Conversely, assume $z\in \Omega $ and for any $\{f_{n}\}\subseteq B(\Omega ), f\in B(\Omega )$ with $\| f_{n}-f\|\rightarrow 0$ , we have $f_{n}(z)\rightarrow f(z)$ , that is, $K_z(f_n)\rightarrow K_z(f).$ Then $K_z$ is continuous on $B(\Omega ).$ Note the continuity of $K_z$ is equivalent to the boundedness of $K_z$ on $B(\Omega )$ , we see that $K_{z}$ is bounded.

A natural question is as follows. Assume $\Omega $ is a bounded domain in ${\mathbb C}^{n}$ , and $B(\Omega )$ is the Banach space of holomorphic functions on $\Omega $ . Then is $K_z$ necessarily bounded?

We know that if $B(\Omega )$ is the Banach space of holomorphic functions on $\Omega $ , due to the fact that any function in $B(\Omega )$ is holomorphic on the entire $\Omega $ , then for arbitrary ${z\in \Omega , K_z}$ is well defined. Although in the case of common classical holomorphic function spaces, evaluation functionals are bounded as long as $K_z$ is well defined, we do not know whether $K_z$ must be bounded on the general Banach space of holomorphic functions on $\Omega $ if $K_z$ is well defined.