Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-26T07:51:52.988Z Has data issue: false hasContentIssue false
  • English
  • Français

Exact coverings of triples with specified longest block length

Part of: Designs and configurations

Published online by Cambridge University Press:  09 April 2009

R. G. Stanton  and
J. L. Allston
R. G. Stanton
Affiliation:
Department of Computer ScienceUniversity of ManitobaWinnipeg, R3T 2N2, Canada
J. L. Allston
Affiliation:
Department of Computer ScienceUniversity of ManitobaWinnipeg, R3T 2N2, Canada
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A minimal (1,3; ν) covering occurs when we have a family of proper subsets selected from ν elements with the property that every triple occurs exactly once in the family and no family of smaller cardinality possesses this property. Woodall developed a lower bound W for the quantity g(k)(1, 3; ν) which represents the cardinality of a minimal family with longest block of length k. The Woodall bound is only accurate in the region when k ≥ ν/2. We develop an expression for the excess of the true value over the Woodall bound and apply this to show that, when k ≥ ν/2, the value of g(1,3; ν) = W + 1 when k is even and W + 1 + 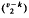when k is odd.

MSC classification

Secondary: 05B30: Other designs, configurations
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 42 , Issue 3 , June 1987 , pp. 409 - 420
Copyright
Copyright © Australian Mathematical Society 1987

References

[1]de Bruijn, N. G. and Erdös, P., ‘On a combinatorial problem’, Nederl. Akad. Wetensch. Indag. Math. 10 (1948), 421–423.Google Scholar
[2]Best, M. R., Brouwer, A. E., McWilliams, F. J., Odlyzko, A. M., and Sloane, N. J. A., ‘Bounds for binary codes of length less than 25’, IEEE Trans. Information Theory 24 (1978), 81–93.CrossRefGoogle Scholar
[3]Hartman, A., Mullin, R. C., and Stinson, D. R., ‘Exact covering configurations and Steiner systems’, J. London Math. Soc. (2) 25 (1982), 193–200.CrossRefGoogle Scholar
[4]Mullin, R. C., Stanton, R. G., and Stinson, D. R., ‘Perfect pair-coverings and an algorithm for certain (1–2) factorizations of the complete graph K2s+1’, Ars Combinatoria 12 (1981), 73–80.Google Scholar
[5]Sloan, N. J. A. and McWilliams, F. J., The Theory of Error-Correcting Codes (North-Holland, Amsterdam, 1977).Google Scholar
[6]Stanton, R. G., ‘Old and new results on perfect coverings (Combinatorial Mathematics IX, Springer-Verlag, Berlin, Heidelberg, New York, 1981), 142–149.Google Scholar
[7]Stanton, R. G., Allston, J. L., and Cowan, D. D., ‘Determination of an exact covering by triples’, Congr. Numer. 31 (1981), 253–258.Google Scholar
[8]Stanton, R. G., Allston, J. L., and Cowan, D. D., ‘Pair-coverings with restricted largest block length’, Ars Combinatoria 11 (1981), 85–98.Google Scholar
[9]Stanton, R. G., Allston, J. L., Eades, P. D., and Cowan, D. D., ‘Computation of the g(1, 3; 20) cover’, J. of Combinatorics, Information, Syst. Sci. 6 (1980), 173–177.Google Scholar
[10]Stanton, R. G. and Dirksen, P. H., ‘Computation of g(1,3;12)’ (Combinatorial Mathematics IV, Springer-Verlag, Berlin, Heidelberg, New York, 1976), 232–234.CrossRefGoogle Scholar
[11]Stanton, R. G., Eades, P. D., van Rees, G. H. J., and Cowan, D. D., ‘Computation of some exact g-coverings’, Utilitas Math. 18 (1980), 269–282.Google Scholar
[12]Stanton, R. G. and Goulden, I. P., ‘Graph factorization, general triple systems, and cyclic triple systems’, Aequationes Math. 22 (1981), 1–28.CrossRefGoogle Scholar
[13]Stanton, R. G. and Kalbfleisch, J. G., ‘The λ − μ problem: λ = 1 and μ = 3’ (Proc. Second Chapel Hill Conf. on Combinatorics, Univ. of North Carolina, 1972), 451–462.Google Scholar
[14]Stanton, R. G. and Kalbfleisch, J. G., ‘Maximal and minimal coverings of (k − 1)-tuples by k–tuples’, Pacific J. Math. 26 (1968), 131–140.Google Scholar
[15]Stanton, R. G. and Stinson, D. R., ‘Perfect pair-coverings with block sizes two, three, and four’, J. of Combinatorics, Information, Syst. Sci. 8 (1983), 21–25.Google Scholar
[16]Stinson, D. R., ‘Applications and generalizations of the variance method in combinatorial designs’, Utilitas Math. 22 (1982), 323–333.Google Scholar
[17]Woodall, D. R., ‘The λ-μ problem’, J. London Math. Soc. 1 (1969), 505–519.Google Scholar