Hostname: page-component-6bf8c574d5-956mj Total loading time: 0 Render date: 2025-02-21T21:33:03.840Z Has data issue: false hasContentIssue false
  • English
  • Français

EXISTENCE OF POSITIVE SOLUTION FOR INDEFINITE KIRCHHOFF EQUATION IN EXTERIOR DOMAINS WITH SUBCRITICAL OR CRITICAL GROWTH

Part of: Elliptic equations and systems Boundary value problems Functional-differential and differential-difference equations Qualitative theory Qualitative behavior

Published online by Cambridge University Press:  23 December 2016

G. M. FIGUEIREDO  and
D. C. DE MORAIS FILHO
G. M. FIGUEIREDO
Affiliation:
Universidade Federal do Pará, Faculdade de Matemática, CEP: 66075-110, Belém - Pa, Brazil email giovany@ufpa.br
D. C. DE MORAIS FILHO*
Affiliation:
Universidade Federal de Campina Grande, Unidade Acadêmica de Matemática, CEP: 58109-970, Campina Grande - Pb, Brazil email daniel@dme.ufcg.edu.br
*
✉daniel@dme.ufcg.edu.br
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Using variational methods and depending on a parameter 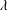$\unicode[STIX]{x1D706}$ we prove the existence of solutions for the following class of nonlocal boundary value problems of Kirchhoff type defined on an exterior domain 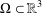$\unicode[STIX]{x1D6FA}\subset \mathbb{R}^{3}$:

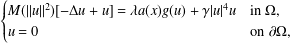$$\begin{eqnarray}\left\{\begin{array}{@{}ll@{}}M(\Vert u\Vert ^{2})[-\unicode[STIX]{x1D6E5}u+u]=\unicode[STIX]{x1D706}a(x)g(u)+\unicode[STIX]{x1D6FE}|u|^{4}u\quad & \text{in }\unicode[STIX]{x1D6FA},\\ u=0\quad & \text{on }\unicode[STIX]{x2202}\unicode[STIX]{x1D6FA},\end{array}\right.\end{eqnarray}$$
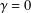for the subcritical case ($\unicode[STIX]{x1D6FE}=0$) and also for the critical case (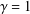$\unicode[STIX]{x1D6FE}=1$).

Keywords

Variational methodsnonlocal problemsKirchhoff equationexterior domain

MSC classification

Primary: 45M20: Positive solutions
Secondary: 35J25: Boundary value problems for second-order elliptic equations 34B18: Positive solutions of nonlinear boundary value problems 34C11: Growth, boundedness 34K12: Growth, boundedness, comparison of solutions
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 103 , Issue 3 , December 2017 , pp. 329 - 340
Copyright
© 2016 Australian Mathematical Publishing Association Inc. 

Footnotes

The first author was partially supported by PROCAD/CASADINHO: 552101/2011-7 and CNPq/PQ 301242/2011-9; the second author was partially supported by PROCAD/Casadinho: 552.464/2011-2 and FNDE-PET/BRAZIL.

References

Alves, C. O., Corrêa, F. J. S. A. and Figueiredo, G. M., ‘On a class of nonlocal elliptic problems with critical growth’, Differ. Equ. Appl. 2 (2010), 409–417.Google Scholar
Alves, C. O., Corrêa, F. J. S. A. and Ma, T. F., ‘Positive solutions for a quasilinear elliptic equation of Kirchhoff type’, Comput. Math. Appl. 49 (2005), 85–93.Google Scholar
Alves, C. O. and Figueiredo, G. M., ‘Nonlinear perturbations of a periodic Kirchhoff equation in ℝ N ’, Nonlinear Anal. 75 (2012), 2750–2759.Google Scholar
Alves, C. O., Freitas, L. R. and Soares, S. H. M., ‘Indefinite quasilinear elliptic equations in exterior domains with exponential critical growth’, Differential Integral Equations 24 (2011), 1047–1062.Google Scholar
Ambrosetti, A. and Rabinowitz, P. H., ‘Dual variational methods in critical point theory and applications’, J. Funct. Anal. 14 (1973), 349–381.CrossRefGoogle Scholar
Arosio, A., ‘On the nonlinear Timoshenko–Kirchhoff beam equation’, Chin. Annal. Math. 20 (1999), 495–506.Google Scholar
Arosio, A., ‘A geometrical nonlinear correction to the Timoshenko beam equation’, Nonlinear Anal. 47 (2001), 729–740.CrossRefGoogle Scholar
Chen, C., Kuo, Y. and Wu, T., ‘The Nehari manifold for a Kirchhoff type problem involving sign-changing weight functions’, J. Differential Equations 250(4) (2011), 1876–1908.Google Scholar
de Morais Filho, D. C. and Miyagaki, O. H., ‘Critical singular problems on unbounded domains’, Abst. Appl. Anal. 6 (2005), 639–653.Google Scholar
Kirchhoff, G., Mechanik (Teubner, Leipzig, 1883).Google Scholar
Lions, P. L., ‘The concentration–compactness principle in the calculus of variations: the limit case’, Rev. Mat. Iberoamericana 1 (1985), 145–201.CrossRefGoogle Scholar
Ma, T. F., ‘Remarks on an elliptic equation of Kirchhoff type’, Nonlinear Anal. 63(5–7) (2005), 1967–1977.Google Scholar
Tehrani, H., ‘Solutions for indefinite semilinear elliptic equations in exterior domains’, J. Math. Anal. Appl. 255 (2001), 308–318.Google Scholar
Willem, M., Minimax Theorems (Birkhäuser, Boston, 1996).Google Scholar