Hostname: page-component-78c5997874-s2hrs Total loading time: 0 Render date: 2024-11-10T16:41:02.314Z Has data issue: false hasContentIssue false
  • English
  • Français

EXPANDER GRAPHS AND SIEVING IN COMBINATORIAL STRUCTURES

Part of: Graph theory Stochastic processes

Published online by Cambridge University Press:  11 January 2018

FLORENT JOUVE  and
JEAN-SÉBASTIEN SERENI
FLORENT JOUVE*
Affiliation:
IMB, Université de Bordeaux, Talence, France email florent.jouve@math.u-bordeaux.fr
JEAN-SÉBASTIEN SERENI
Affiliation:
C.N.R.S. (LORIA), Vandœuvre-lès-Nancy, France email sereni@kam.mff.cuni.cz
*
✉ florent.jouve@math.u-bordeaux.fr
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We prove a general large-sieve statement in the context of random walks on subgraphs of a given graph. This can be seen as a generalization of previously known results where one performs a random walk on a group enjoying a strong spectral gap property. In such a context the point is to exhibit a strong uniform expansion property for a suitable family of Cayley graphs on quotients. In our combinatorial approach, this is replaced by a result of Alon–Roichman about expanding properties of random Cayley graphs. Applying the general setting we show, for instance, that with high probability (in a strong explicit sense) random coloured subsets of integers contain monochromatic (nonempty) subsets summing to 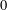 $0$ , and that a random colouring of the edges of a complete graph contains a monochromatic triangle.

Keywords

random walksgroupsgraphssieve

MSC classification

Primary: 60G50: Sums of independent random variables; random walks
Secondary: 05C25: Graphs and abstract algebra (groups, rings, fields, etc.)
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 105 , Issue 1 , August 2018 , pp. 79 - 102
Copyright
© 2018 Australian Mathematical Publishing Association Inc. 

References

Alon, N. and Lubotzky, A., ‘Semi-direct product in groups and zig–zag product in graphs: connections and applications (extended abstract)’, in: 42nd IEEE Sympos. Foundations of Computer Science (Las Vegas, NV, 2001) (IEEE Computer Society, Los Alamitos, CA, 2001), 630–637.Google Scholar
Alon, N. and Rödl, V., ‘Sharp bounds for some multicolor Ramsey numbers’, Combinatorica 25(2) (2005), 125–141.Google Scholar
Alon, N. and Roichman, Y., ‘Random Cayley graphs and expanders’, Random Structures Algorithms 5(2) (1994), 271–284.CrossRefGoogle Scholar
Bourgain, J., Gamburd, A. and Sarnak, P., ‘Affine linear sieve, expanders, and sum-product’, Invent. Math. 179(3) (2010), 559–644.CrossRefGoogle Scholar
Christofides, D. and Markström, K., ‘Expansion properties of random Cayley graphs and vertex transitive graphs via matrix martingales’, Random Structures Algorithms 32(1) (2008), 88–100.Google Scholar
Davidoff, G., Sarnak, P. and Valette, A., Elementary Number Theory, Group Theory, and Ramanujan Graphs, London Mathematical Society Student Texts, 55 (Cambridge University Press, Cambridge, 2003).Google Scholar
Golsefidy, A. S. and Varjú, P. P., ‘Expansion in perfect groups’, Geom. Funct. Anal. 6(22) (2012), 1832–1891.Google Scholar
Jouve, F., Kowalski, E. and Zywina, D., ‘Splitting fields of characteristic polynomials of random elements in arithmetic groups’, Israel J. Math. 193(1) (2013), 263–307.CrossRefGoogle Scholar
Kowalski, E., The Large Sieve and its Applications: Arithmetic Geometry, Random Walks and Discrete Groups, Cambridge Tracts in Mathematics, 175 (Cambridge University Press, Cambridge, 2008).Google Scholar
Landau, Z. and Russell, A., ‘Random Cayley graphs are expanders: a simple proof of the Alon–Roichman theorem’, Electron. J. Combin. 11(1) (2004), Research Paper 62, 6.Google Scholar
Loh, P.-S. and Schulman, L. J., ‘Improved expansion of random Cayley graphs’, Discrete Math. Theor. Comput. Sci. 2(6) (2004), 523–528 (electronic).Google Scholar
Lubotzky, A. and Meiri, C., ‘Sieve methods in group theory I: powers in linear groups’, J. Amer. Math. Soc. 25(4) (2012), 1119–1148.Google Scholar
Lubotzky, A. and Zuk, A., ‘On property $(\unicode[STIX]{x1D70F})$ ’, Preprint, 2002.Google Scholar
Molloy, M. and Reed, B., Graph Colouring and the Probabilistic Method, Algorithms and Combinatorics, 23 (Springer, Berlin, 2002).Google Scholar
Ramsey, F. P., ‘On a problem of formal logic’, Proc. Lond. Math. Soc. (1) S2‐30 (1930), 264–286.Google Scholar
van der Waerden, B. L., ‘Beweis einer Baudetschen Vermutung’, Nieuw Arch. Wiskd. 15(1) (1927), 212–216.Google Scholar