Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-29T02:27:14.153Z Has data issue: false hasContentIssue false
  • English
  • Français

Families of partial representing sets

Published online by Cambridge University Press:  09 April 2009

Kevin P. Balanda
Kevin P. Balanda
Affiliation:
Department of Mathematics University of QueenslandSt. Lucia, Qld 4067, Australia
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Assume GCH. Let κ, μ, Σ be cardinals, with κ infinite. Let 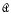be a family consisting of λ pairwise almost disjoint subsets of Σ each of size κ, whose union is Σ. In this note it is shown that for each μ with 1 ≤ μ ≤min(λ, Σ), there is a “large” almost disjoint family 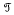of μ-sized subsets of Σ, each member of 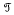having non-empty intersection with at least μ members of the family .

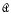Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 38 , Issue 2 , April 1985 , pp. 198 - 206
Copyright
Copyright © Australian Mathematical Society 1985

References

[1]Balanda, K. P., ‘Maximally almost disjoint families of representing sets’, Math. Proc. Cambridge Philos. Soc. 93 (1983), 1–7.Google Scholar
[2]Balanda, K. P., ‘Almost disjoint families of representing sets’, Z. Math. Logik Grundlag. Math., to appear.Google Scholar
[3]Baumgartner, J. E., ‘Almost-disjoint sets, the dense set problem and partition calculus’, Ann. Math. Logic 9 (1976), 401–439.Google Scholar
[4]Erdös, P. and Rado, R., ‘Intersection theorems for systems of sets I’, J. London Math. Soc. 44 (1969), 467–479.Google Scholar
[5]Williams, N. H., Combinatorial set theory (North-Holland, Amsterdam, 1977).Google Scholar