Hostname: page-component-78c5997874-4rdpn Total loading time: 0 Render date: 2024-11-10T17:48:30.475Z Has data issue: false hasContentIssue false
  • English
  • Français

FINITE NORMAL 2-GEODESIC TRANSITIVE CAYLEY GRAPHS

Part of: Permutation groups Algebraic combinatorics

Published online by Cambridge University Press:  16 March 2016

WEI JIN
WEI JIN*
Affiliation:
School of Statistics, Jiangxi University of Finance and Economics, Nanchang, Jiangxi 330013, PR China Research Center of Applied Statistics, Jiangxi University of Finance and Economics, Nanchang, Jiangxi 330013, PR China email jinwei@jxufe.edu.cn
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

For an odd prime 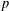$p$, a 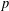$p$-transposition group is a group generated by a set of involutions such that the product of any two has order 2 or 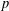$p$. We first classify a family of 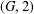$(G,2)$-geodesic transitive Cayley graphs 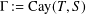${\rm\Gamma}:=\text{Cay}(T,S)$ where 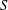$S$ is a set of involutions and 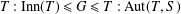$T:\text{Inn}(T)\leq G\leq T:\text{Aut}(T,S)$. In this case, $T$ is either an elementary abelian 2-group or a 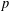$p$-transposition group. Then under the further assumption that 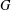$G$ acts quasiprimitively on the vertex set of 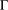${\rm\Gamma}$, we prove that: (1) if 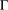${\rm\Gamma}$ is not 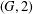$(G,2)$-arc transitive, then this quasiprimitive action is the holomorph affine type; (2) if 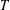$T$ is a 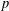$p$-transposition group and 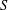$S$ is a conjugacy class, then 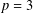$p=3$ and 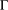${\rm\Gamma}$ is 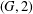$(G,2)$-arc transitive.

Keywords

2-geodesic transitive graphCayley graphautomorphism group

MSC classification

Primary: 05E18: Group actions on combinatorial structures
Secondary: 20B25: Finite automorphism groups of algebraic, geometric, or combinatorial structures
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 100 , Issue 3 , June 2016 , pp. 338 - 348
Copyright
© 2016 Australian Mathematical Publishing Association Inc. 

References

Alspach, B., Conder, M., Marušič, D. and Xu, M. Y., ‘A classification of 2-arc-transitive circulants’, J. Algebraic Combin. 5 (1996), 83–86.CrossRefGoogle Scholar
Aschbacher, M., ‘On finite groups generated by odd transpositions I’, Math. Z. 127 (1972), 45–56.Google Scholar
Aschbacher, M., ‘On finite groups generated by odd transpositions II’, J. Algebra 26 (1973), 451–459.Google Scholar
Devillers, A., Jin, W., Li, C. H. and Praeger, C. E., ‘Line graphs and geodesic transitivity’, Ars Math. Contemp. 6 (2013), 13–20.CrossRefGoogle Scholar
Devillers, A., Jin, W., Li, C. H. and Praeger, C. E., ‘Local 2-geodesic transitivity and clique graphs’, J. Combin. Theory Ser. A 120 (2013), 500–508.Google Scholar
Devillers, A., Jin, W., Li, C. H. and Praeger, C. E., ‘On normal 2-geodesic transitive Cayley graphs’, J. Algebraic Combin. 39 (2014), 903–908.CrossRefGoogle Scholar
Devillers, A., Jin, W., Li, C. H. and Praeger, C. E., ‘Finite 2-geodesic transitive graphs of prime valency’, J. Graph Theory 80 (2015), 18–27.CrossRefGoogle Scholar
Du, S. F., Wang, R. J. and Xu, M. Y., ‘On the normality of Cayley digraphs of order twice a prime’, Australas. J. Combin. 18 (1998), 227–234.Google Scholar
Fischer, B., ‘Finite groups generated by 3-transpositions I’, Invent. Math. 13 (1971), 232–246.CrossRefGoogle Scholar
Godsil, C. D., ‘On the full automorphism group of a graph’, Combinatorica 1 (1981), 243–256.CrossRefGoogle Scholar
Gorenstein, D., Finite Simple Groups—An Introduction to Their Classification (Plenum Press, New York, 1982).Google Scholar
Ivanov, A. A. and Praeger, C. E., ‘On finite affine 2-arc transitive graphs’, European J. Combin. 14 (1993), 421–444.Google Scholar
Kwak, J. H. and Oh, J. M., ‘One-regular normal Cayley graphs on dihedral groups of valency 4 or 6 with cyclic vertex stabilizer’, Acta Math. Sin. (Engl. Ser.) 22 (2006), 1305–1320.CrossRefGoogle Scholar
Li, C. H. and Pan, J. M., ‘Finite 2-arc-transitive abelian Cayley graphs’, European J. Combin. 29 (2008), 148–158.CrossRefGoogle Scholar
Lu, Z. P. and Xu, M. Y., ‘On the normality of Cayley graphs of order pq’, Australas. J. Combin. 27 (2003), 81–93.Google Scholar
Marušič, D., ‘On 2-arc-transitivity of Cayley graphs’, J. Combin. Theory Ser. B 87 (2003), 162–196.Google Scholar
Praeger, C. E., ‘An O’Nan Scott theorem for finite quasiprimitive permutation groups and an application to 2-arc transitive graphs’, J. Lond. Math. Soc. (2) 47 (1993), 227–239.CrossRefGoogle Scholar
Praeger, C. E., ‘On a reduction theorem for finite, bipartite, 2-arc transitive graphs’, Australas. J. Combin. 7 (1993), 21–36.Google Scholar
Praeger, C. E., ‘Finite normal edge-transitive Cayley graphs’, Bull. Aust. Math. Soc. 60 (1999), 207–220.Google Scholar
Tutte, W. T., ‘A family of cubical graphs’, Proc. Cambridge Philos. Soc. 43 (1947), 459–474.CrossRefGoogle Scholar
Tutte, W. T., ‘On the symmetry of cubic graphs’, Canad. J. Math. 11 (1959), 621–624.CrossRefGoogle Scholar
Weiss, R., ‘The non-existence of 8-transitive graphs’, Combinatorica 1 (1981), 309–311.CrossRefGoogle Scholar
Xu, M. Y., ‘Automorphism groups and isomorphisms of Cayley digraphs’, Discrete Math. 182 (1998), 309–319.Google Scholar