Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-26T07:51:24.071Z Has data issue: false hasContentIssue false
  • English
  • Français

FINITE-DIMENSIONAL ORDERED VECTOR SPACES WITH RIESZ INTERPOLATION AND EFFROS–SHEN’S UNIMODULARITY CONJECTURE

Part of: Topological linear spaces and related structures Lattices Ordered structures

Published online by Cambridge University Press:  13 May 2016

AARON TIKUISIS Open the ORCID record for AARON TIKUISIS [Opens in a new window]
AARON TIKUISIS*
Affiliation:
Institute of Mathematics, University of Aberdeen, Aberdeen, AB24 3UE, UK email a.tikuisis@abdn.ac.uk
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

It is shown that, for any field 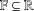$\mathbb{F}\subseteq \mathbb{R}$, any ordered vector space structure of 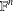$\mathbb{F}^{n}$ with Riesz interpolation is given by an inductive limit of a sequence with finite stages 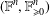$(\mathbb{F}^{n},\mathbb{F}_{\geq 0}^{n})$ (where $n$ does not change). This relates to a conjecture of Effros and Shen, since disproven, which is given by the same statement, except with 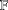$\mathbb{F}$ replaced by the integers, 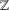$\mathbb{Z}$. Indeed, it shows that although Effros and Shen’s conjecture is false, it is true after tensoring with 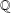$\mathbb{Q}$.

Keywords

dimension groupsRiesz interpolationordered vector spacesunimodularity conjecturesimplicial groupslattice-ordered groups

MSC classification

Primary: 46A40: Ordered topological linear spaces, vector lattices
Secondary: 06B75: Generalizations of lattices 06F20: Ordered abelian groups, Riesz groups, ordered linear spaces
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 101 , Issue 2 , October 2016 , pp. 277 - 287
Copyright
© 2016 Australian Mathematical Publishing Association Inc. 

References

Birkhoff, G., ‘Lattice-ordered groups’, Ann. of Math. (2) 43 (1942), 298–331.Google Scholar
Effros, E. G., Handelman, D. E. and Shen, C. L., ‘Dimension groups and their affine representations’, Amer. J. Math. 102(2) (1980), 385–407.Google Scholar
Effros, E. G. and Shen, C. L., ‘Dimension groups and finite difference equations’, J. Operator Theory 2(2) (1979), 215–231.Google Scholar
Goodearl, K. R., Partially Ordered Abelian Groups with Interpolation, Mathematical Surveys and Monographs, 20 (American Mathematical Society, Providence, RI, 1986).Google Scholar
Goodearl, K. R. and Handelman, D. E., ‘Tensor products of dimension groups and K 0 of unit-regular rings’, Canad. J. Math. 38(3) (1986), 633–658.Google Scholar
Handelman, D., ‘Real dimension groups’, Canad. Math. Bull. 56(3) (2013), 551–563.Google Scholar
Maloney, G. R. and Tikuisis, A., ‘A classification of finite rank dimension groups by their representations in ordered real vector spaces’, J. Funct. Anal. 260(11) (2011), 3404–3428.CrossRefGoogle Scholar
Riedel, N., ‘A counterexample to the unimodular conjecture on finitely generated dimension groups’, Proc. Amer. Math. Soc. 83(1) (1981), 11–15.CrossRefGoogle Scholar