Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Kovács, L. G.
and
Newman, M. F.
1974.
Proceedings of the Second International Conference on The Theory of Groups.
Vol. 372,
Issue. ,
p.
417.
Kovács, L. G.
and
Newman, M. F.
1974.
Proceedings of the Second International Conference on the Theory of Groups.
Vol. 372,
Issue. ,
p.
417.
Gupta, Narain
and
Levin, Frank
1974.
Generating groups of certain soluble varieties.
Journal of the Australian Mathematical Society,
Vol. 17,
Issue. 2,
p.
222.
Gupta, Narain
and
Levin, Frank
1976.
Separating laws for free centre -by -metabelian nilpotent groups.
Communications in Algebra,
Vol. 4,
Issue. 3,
p.
249.
Gupta, N.D
and
Passi, I.B.S
1976.
Some properties of fox subgroups of free groups.
Journal of Algebra,
Vol. 43,
Issue. 1,
p.
198.
Gupta, N. D.
and
Wehrfritz, B. A. F.
1976.
Some residual properties of certain nilpotent-by-Abelian groups.
Archiv der Mathematik,
Vol. 27,
Issue. 1,
p.
449.
Gupta, Chander Kanta
1978.
Subgroups of free groups induced by certain products of augmentation ideals.
Communications in Algebra,
Vol. 6,
Issue. 12,
p.
1231.
Gupta, Chander Kanta
and
Gupta, Narain Datt
1978.
Generalized Magnus embeddings and some applications.
Mathematische Zeitschrift,
Vol. 160,
Issue. 1,
p.
75.
Thomson, Michael W.
1979.
Representations of certain verbal wreath products by matrices.
Mathematische Zeitschrift,
Vol. 167,
Issue. 3,
p.
239.
Stöhr, R.
1980.
Freie Produkte torsionsfreier abelscher Gruppen in der Varietät der zentralen Erweiterungen metabelscher Gruppen.
Mathematische Nachrichten,
Vol. 96,
Issue. 1,
p.
271.
Noskov, G. A.
Remeslennikov, V. N.
and
Roman'kov, V. A.
1982.
Infinite groups.
Journal of Soviet Mathematics,
Vol. 18,
Issue. 5,
p.
669.
St�hr, Ralph
1984.
On Gupta representations of central extensions.
Mathematische Zeitschrift,
Vol. 187,
Issue. 2,
p.
259.
Kuz'min, Yu. V.
1985.
Elements of order 2 in a free centrally solvable group.
Mathematical Notes of the Academy of Sciences of the USSR,
Vol. 37,
Issue. 5,
p.
350.
Gupta, N. D.
Hurley, T. C.
and
Levin, F.
1985.
On the lower central factors of free centre-by-metabelian groups.
Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics,
Vol. 38,
Issue. 1,
p.
65.
Drensky, Vesselin
1986.
Torsion in the additive group of relatively free Lie rings.
Bulletin of the Australian Mathematical Society,
Vol. 33,
Issue. 1,
p.
81.
Stöhr, Ralph
1987.
On torsion in free central extensions of some torsion-free groups.
Journal of Pure and Applied Algebra,
Vol. 46,
Issue. 2-3,
p.
249.
Kuz’min, Yu V.
1988.
Homology theory of free abelianized extensions.
Communications in Algebra,
Vol. 16,
Issue. 12,
p.
2447.
Zerck, Rainer
1989.
On the homology of the higher relation modules.
Journal of Pure and Applied Algebra,
Vol. 58,
Issue. 3,
p.
305.
Stöhr, Ralph
1989.
On elements of order four in certain free central extensions of groups.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 106,
Issue. 1,
p.
13.
Gupta, C. K.
Gupta, N. D.
and
Levin, F.
1989.
On conjugacy p-separability of free centre-by-metabelian groups.
Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics,
Vol. 47,
Issue. 2,
p.
334.


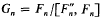 be the free centre-by-metabelian group of rank
be the free centre-by-metabelian group of rank 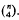 . More precisely, H
. More precisely, H