Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-10T21:14:56.136Z Has data issue: false hasContentIssue false
  • English
  • Français

Free Lie algebras as modules for symmetric groups

Part of: Representation theory of groups Lie algebras and Lie superalgebras

Published online by Cambridge University Press:  09 April 2009

R. M. Bryant ,
L. G. Kovács  and
Ralph Stöhr
R. M. Bryant
Affiliation:
UMIST PO Box 88 Manchester M60 1QD England e-mail: bryamt@umist.ac.uk e-mail: r.stohr@umist.ac.uk
L. G. Kovács
Affiliation:
Australian National University Canberra ACT 0200 Australia e-mail: kovacs@maths.anu.edu.au
Ralph Stöhr
Affiliation:
UMIST PO Box 88 Manchester M60 1QD England e-mail: bryamt@umist.ac.uk e-mail: r.stohr@umist.ac.uk
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let r be a positive integer, F a field of odd prime characteristic p, and L the free Lie algebra of rank r over F. Consider L a module for the symmetric group 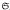, of all permutations of a free generating set of L. The homogeneous components Ln of L are finite dimensional submodules, and L is their direct sum. For p ≤ r ≤ 2p, the main results of this paper identify the non-porojective indecomposable direct summands of the Ln as Specht modules or dual Specht modules corresponding to certain partitions. For the case r = p, the multiplicities of these indecomposables in the direct decompositions of the Ln are also determined, as are the multiplicities of the projective indecomposables. (Corresponding results for p = 2 have been obtained elsewhere.)

MSC classification

Secondary: 17B01: Identities, free Lie (super)algebras 20C30: Representations of finite symmetric groups
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 67 , Issue 2 , October 1999 , pp. 143 - 156
Copyright
Copyright © Australian Mathematical Society 1999

References

[1]Alperin, J. L., Local representation theory, Cambridge Studies in Advanced Math. 11 (Cambridge University Press, Cambridge, 1986).CrossRefGoogle Scholar
[2]Bourbaki, N., Groupes et algébres de Lie, Chap. II, III, Actualités Sci. Indust. 1349 (Hermann, Paris, 1972).Google Scholar
[3]Brandt, A. J., ‘The free Lie ring and Lie representations of the full linear group’, Trans. Amer. Math. Soc. 56 (1944), 528–536.CrossRefGoogle Scholar
[4]Bryant, R. M. and Stöhr, R., ‘Fixed points of automorphisms of free Lie algebras’, Arch. Math. 67 (1966), 281–289.CrossRefGoogle Scholar
[5]Bryant, R. M., ‘On the module structure of free Lie algebras’, Trans. Amer. Math. Soc., to appear.Google Scholar
[6]Green, J. A., Vorlesungen über modulare Darstellungstheorie endicher Gruppen, Vorlesungen ausdem mathematischen Institut Giessen, Heft 2 (Manuskript: Wolfgang Hamernik) (Mathematisches Institut Giessen, Universität Giessen, Giessen, 1974).Google Scholar
[7]James, G. D., The representation theory of the symmetric groups, Lecture Notes in Math. 682 (Springer-Verlag, Berlin, 1978).CrossRefGoogle Scholar
[8]Kovács, L. G. and Stöhr, R., ‘Module structure of the free Lie ring on three generators’, Arch. Math. 72 (1999), to appear.Google Scholar
[9]Nakayama, T., ‘On some modular properties of irreducible representations of symmetric groups, II’, Japan. J. Math. 17 (1940), 411–423.CrossRefGoogle Scholar
[10]Wall, G. E., ‘On the Lie ring of a group of prime exponent’, in: Proceedings of the second international conference on the theory of groups (ed. Newman, M. F.), Lecture Notes in Math. 372 (Springer-Verlag, Berlin, 1974) pp. 667–690.CrossRefGoogle Scholar
[11]Witt, E., ‘Die Unterringe der freien Lieschen Ringe’, Math. Z. 64 (1956), 195–216.CrossRefGoogle Scholar