Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-26T16:54:47.359Z Has data issue: false hasContentIssue false
  • English
  • Français

FROBENIUS CIRCULANT GRAPHS OF VALENCY FOUR

Part of: Graph theory Operations research and management science Computer system organization

Published online by Cambridge University Press:  01 October 2008

ALISON THOMSON  and
SANMING ZHOU
ALISON THOMSON
Affiliation:
Department of Mathematics and Statistics, The University of Melbourne, Parkville, VIC 3010, Australia (email: a.thomson@ms.unimelb.edu.au)
SANMING ZHOU*
Affiliation:
Department of Mathematics and Statistics, The University of Melbourne, Parkville, VIC 3010, Australia (email: smzhou@ms.unimelb.edu.au)
*
✉For correspondence; e-mail: smzhou@ms.unimelb.edu.au
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

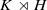A first kind Frobenius graph is a Cayley graph Cay(K,S) on the Frobenius kernel of a Frobenius group such that S=aH for some a∈K with 〈aH〉=K, where H is of even order or a is an involution. It is known that such graphs admit ‘perfect’ routing and gossiping schemes. A circulant graph is a Cayley graph on a cyclic group of order at least three. Since circulant graphs are widely used as models for interconnection networks, it is thus highly desirable to characterize those which are Frobenius of the first kind. In this paper we first give such a characterization for connected 4-valent circulant graphs, and then describe optimal routing and gossiping schemes for those which are first kind Frobenius graphs. Examples of such graphs include the 4-valent circulant graph with a given diameter and maximum possible order.

Keywords

Cayley graphcirculant graphmulti-loop networkdouble-loop networkFrobenius groupFrobenius graphcomplete rotationgossipingminimum gossip timeroutingedge-forwarding indexarc-forwarding index

MSC classification

Secondary: 05C25: Graphs and abstract algebra (groups, rings, fields, etc.) 68M10: Network design and communication 90B18: Communication networks
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 85 , Issue 2 , October 2008 , pp. 269 - 282
Copyright
Copyright © 2008 Australian Mathematical Society

Footnotes

Alison Thomson was supported by a Postgraduate Award of the Australian Government. Sanming Zhou was supported by a Discovery Project Grant of the Australian Research Council.

References

[1]Akers, Sheldon B. and Krishnamurthy, Balakrishnan, ‘A group-theoretic model for symmetric interconnection networks’, IEEE Trans. Comput. 38(4) (1989), 555–566.CrossRefGoogle Scholar
[2]Annexstein, Fred, Baumslag, Marc and Rosenberg, Arnold, ‘Group action graphs and parallel architectures’, SIAM J. Comput. 19(3) (1990), 544–569.CrossRefGoogle Scholar
[3]Bermond, Jean-Claude, Kodate, Takako and Pérennes, Stéphane, Gossiping in Cayley Graphs by Packets (8th Franco-Japanese and 4th Franco-Chinese Conf. on Combinatorial Computer Science, Brest, July 1995), Lecture Notes in Computer Science, 1120 (Springer, Berlin, 1996), pp. 301–315.Google Scholar
[4]Biggs, Norman, Algebraic Graph Theory, 2nd edn, Cambridge Mathematical Library (Cambridge University Press, Cambridge, 1993).Google Scholar
[5]Boesch, Francis T. and Wang, Jhing Fa, ‘Reliable circulant networks with minimum transmission delay’, IEEE Trans. Circuits Syst. 32 (1985), 1286–1291.CrossRefGoogle Scholar
[6]Dixon, John D. and Mortimer, Brian, Permutation Groups (Springer, New York, 1996).CrossRefGoogle Scholar
[7]Fang, Xin Gui, Li, Cai Heng and Praeger, Cheryl E., ‘On orbital regular graphs and Frobenius graphs’, Discrete Math. 182 (1998), 85–99.CrossRefGoogle Scholar
[8]Heydemann, Marie-Claude, ‘Cayley graphs and interconnection networks’, in: Graph Symmetry (eds. G. Hahn and G. Sabidussi) (Kluwer Academic Publishing, Dordrecht, 1997), pp. 167–224.CrossRefGoogle Scholar
[9]Heydemann, Marie-Claude, Marlin, Nausica and Pérenes, Stéphane, ‘Complete rotations in Cayley graphs’, European J. Combin. 22 (2001), 179–196.Google Scholar
[10]Heydemann, Marie-Claude, Meyer, J.-C. and Sotteau, D., ‘On forwarding indices of networks’, Discrete Appl. Math. 23 (1989), 103–123.CrossRefGoogle Scholar
[11]Hwang, F. K., ‘A survey on multi-loop networks’, Theoret. Comput. Sci. 299 (2003), 107–121.CrossRefGoogle Scholar
[12]Ireland, Kenneth and Rosen, Michael, A Classical Introduction to Modern Number Theory (Springer, New York, 1982).CrossRefGoogle Scholar
[13]Li, Cai Heng, ‘On isomorphisms of finite Cayley graphs—a survey’, Discrete Math. 256(1–2) (2002), 301–334.CrossRefGoogle Scholar
[14]Lim, Tim Khoon and Praeger, Cheryl E., ‘Finding optimal routings in Hamming graphs’, European J. Combin. 23 (2002), 1033–1041.Google Scholar
[15]Narayanan, L., Opatrny, J. and Sotteau, D., ‘All-to-all optical routing in chordal rings of degree 4’, Algorithmica 31(2) (2001), 155–178.CrossRefGoogle Scholar
[16]Niven, Ivan and Zuckerman, Herbert S., An Introduction to the Theory of Numbers (John Wiley & Sons, New York, 1980).Google Scholar
[17]Rose, John S., A Course on Group Theory (Cambridge University Press, Cambridge, 1978).Google Scholar
[18]Scott, W. R., Group Theory (Prentice-Hall, Englewood Cliffs, NJ, 1964).Google Scholar
[19]Solé, Patrick, ‘The edge-forwarding index of orbital regular graphs’, Discrete Math. 130(1–3) (1994), 171–176.CrossRefGoogle Scholar
[20]Thomson, Alison and Zhou, Sanming, Gossiping and routing in undirected triple-loop networks, submitted.Google Scholar
[21]Wong, C. K. and Coppersmith, Don, ‘A combinatorial problem related to multimodule memory organizations’, J. Assoc. Comp. Mach. 21(3) (1974), 392–402.CrossRefGoogle Scholar
[22]Yebra, J. L. A., Fiol, M. A., Morillo, P. and Alegre, I., ‘The diameter of undirected graphs associated to plane tessellations’, Ars Combin. 20-B (1985), 159–171.Google Scholar
[23]Zaragoza, M., Liestman, A. L. and Opatrny, J., ‘Network properties of double and triple fixed step graphs’, Int. J. Found. Comput. Sci. 9 (1998), 57–76.Google Scholar
[24]Žerovnik, Janez and Pisanski, Tomaž, ‘Computing the diameter in multi-loop networks’, J. Algorithms 14 (1993), 226–243.CrossRefGoogle Scholar
[25]Zhou, Sanming, ‘A class of arc-transitive Cayley graphs as models for interconnection networks’, SIAM J. Discrete Math. to appear.Google Scholar