Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Kahane, Jean-Pierre
1986.
Géza Freud and lacunary Fourier series.
Journal of Approximation Theory,
Vol. 46,
Issue. 1,
p.
51.


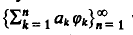 where ф
where ф