Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-13T03:41:56.118Z Has data issue: false hasContentIssue false
  • English
  • Français

GRADIENT FLOWS OF HIGHER ORDER YANG–MILLS–HIGGS FUNCTIONALS

Part of: Variational problems in infinite-dimensional spaces Quantum field theory; related classical field theories Calculus on manifolds; nonlinear operators

Published online by Cambridge University Press:  31 May 2021

PAN ZHANG
PAN ZHANG*
Affiliation:
School of Mathematical Sciences, Anhui University, Hefei230601, PR China
*
e-mail: panzhang20100@ahu.edu.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, we define a family of functionals generalizing the Yang–Mills–Higgs functionals on a closed Riemannian manifold. Then we prove the short-time existence of the corresponding gradient flow by a gauge-fixing technique. The lack of a maximum principle for the higher order operator brings us a lot of inconvenience during the estimates for the Higgs field. We observe that the 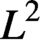$L^2$ -bound of the Higgs field is enough for energy estimates in four dimensions and we show that, provided the order of derivatives appearing in the higher order Yang–Mills–Higgs functionals is strictly greater than one, solutions to the gradient flow do not hit any finite-time singularities. As for the Yang–Mills–Higgs k-functional with Higgs self-interaction, we show that, provided 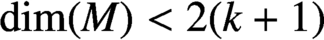$\dim (M)<2(k+1)$ , for every smooth initial data the associated gradient flow admits long-time existence. The proof depends on local 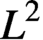$L^2$ -derivative estimates, energy estimates and blow-up analysis.

Keywords

blow-up analysisenergy estimateshigher order Yang–Mills–Higgs flowhigher order Yang–Mills–Higgs functionalL2-estimates

MSC classification

Primary: 58C99: None of the above, but in this section
Secondary: 58E15: Application to extremal problems in several variables; Yang-Mills functionals , etc. 81T13: Yang-Mills and other gauge theories
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 113 , Issue 2 , October 2022 , pp. 257 - 287
Check for updates
Copyright
© 2021 Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Communicated by Graeme Wilkin

The author is supported by the Natural Science Foundation of Universities of Anhui Province (Grant Number K120431039). The author is partially supported by the National Natural Science Foundation of China (Grant Numbers 11625106, 11721101, 12001548 and 11701580). The research is partially supported by the project ‘Analysis and Geometry on Bundle’ of the Ministry of Science and Technology of the People’s Republic of China (Grant Number SQ2020YFA070080).

References

Afuni, A., ‘Local monotonicity for the Yang–Mills–Higgs flow’, Calc. Var. Partial Differential Equations 55(1) (2016), Article 13.CrossRefGoogle Scholar
Atiyah, M. F. and Bott, R., ‘The Yang–Mills equations over Riemann surfaces’, Philos. Trans. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 308(1505) (1983), 523–615.Google Scholar
Bahuaud, E. and Helliwell, D., ‘Short-time existence for some higher-order geometric flows’, Comm. Partial Differential Equations 36(12) (2011), 2189–2207.CrossRefGoogle Scholar
Chang, C. K., Ding, W. Y. and Ye, R., ‘Finite-time blow-up of the heat flow of harmonic maps from surfaces’, J. Differential Geom. 36(2) (1992), 507–515.CrossRefGoogle Scholar
Daskalopoulos, G., ‘The topology of the space of stable bundles on a compact Riemann surface’, J. Differential Geom. 36(3) (1992), 699–746.CrossRefGoogle Scholar
Daskalopoulos, G., ‘Convergence properties of the Yang–Mills flow on Kähler surfaces’, J. reine angew. Math. 575 (2004), 69–99.Google Scholar
Daskalopoulos, G. and Wentworth, R., ‘On the blow-up set of the Yang–Mills flow on Kähler surfaces’, Math. Z. 256(2) (2007), 301–310.CrossRefGoogle Scholar
De Giorgi, E., ‘Congetture riguardanti alcuni problemi di evoluzione’, Duke Math. J. 81(2) (1996), 255–268.CrossRefGoogle Scholar
Donaldson, S. K., ‘Anti self-dual Yang–Mills connections over complex algebraic surfaces and stable vector bundles’, Proc. Lond. Math. Soc. 3(1) (1985), 1–26.CrossRefGoogle Scholar
Donaldson, S. K., ‘Infinite determinants, stable bundles and curvature’, Duke Math. J. 54(1) (1987), 231–247.CrossRefGoogle Scholar
Donaldson, S. K. and Kronheimer, P. B., The Geometry of Four-Manifolds (Oxford University Press, Oxford, 1997).Google Scholar
Escher, J., Mayer, U. F. and Simonett, G., ‘The surface diffusion flow for immersed hypersurfaces’, SIAM J. Math. Anal. 29(6) (1998), 1419–1433.CrossRefGoogle Scholar
Hassell, A., ‘The Yang–Mills–Higgs heat flow on R3’, J. Funct. Anal. 111(2) (1993), 431–448.CrossRefGoogle Scholar
Hitchin, N. J., ‘The self-duality equations on a Riemann surface’, Proc. Lond. Math. Soc. 3(1) (1987), 59–126.CrossRefGoogle Scholar
Hong, M. C., ‘Heat flow for the Yang–Mills–Higgs field and the Hermitian Yang–Mills–Higgs metric’, Ann. Global Anal. Geom. 20(1) (2001), 23–46.CrossRefGoogle Scholar
Hong, M. C. and Schabrun, L., ‘Global existence for the Seiberg–Witten flow’, Comm. Anal. Geom. 18(3) (2010), 433–473.CrossRefGoogle Scholar
Hong, M. C. and Tian, G., ‘Asymptotical behaviour of the Yang–Mills flow and singular Yang–Mills connections’, Math. Ann. 330(3) (2004), 441–472.CrossRefGoogle Scholar
Jacob, A., ‘The limit of the Yang–Mills flow on semi-stable bundles’, J. Reine Angew. Math. 709 (2015), 1–13.CrossRefGoogle Scholar
Jaffe, A. and Taubes, C. H., Vortices and Monopoles: Structure of Static Gauge Theories (Birkhäuser, Basel, 1980).Google Scholar
Jia, Z. L. and Wang, Y. D., ‘Higher-order geometric flow of hypersurfaces in a Riemannian manifold’, Int. J. Math. 30(13) (2019), 1940005.CrossRefGoogle Scholar
Kelleher, C., ‘Higher order Yang–Mills flow’, Calc. Var. Partial Differential Equations 58(3) (2019), 1–45.CrossRefGoogle Scholar
Kotschwar, B., ‘An energy approach to uniqueness for higher-order geometric flows’, J. Geom. Anal. 26(4) (2016), 3344–3368.CrossRefGoogle Scholar
Kuwert, E. and Schätzle, R., ‘The Willmore flow with small initial energy’, J. Differential Geom. 57(3) (2001), 409–441.CrossRefGoogle Scholar
Kuwert, E. and Schätzle, R., ‘Gradient flow for the Willmore functional’, Comm. Anal. Geom. 10(2) (2002), 307–339.CrossRefGoogle Scholar
Li, J. Y., Zhang, C. J. and Zhang, X., ‘The limit of the Hermitian–Yang–Mills flow on reflexive sheaves’, Adv. Math. 325 (2018), 165–214.CrossRefGoogle Scholar
Li, J. Y., Zhang, C. J. and Zhang, X., ‘A note on curvature estimate of the Hermitian–Yang–Mills flow’, Commun. Math. Stat. 6(3) (2018), 319–358.CrossRefGoogle Scholar
Li, J. Y. and Zhang, X., ‘The gradient flow of Higgs pairs’, J. Eur. Math. Soc. 13(5) (2011), 1373–1422.CrossRefGoogle Scholar
Liu, D. and Zhang, P., ‘Hermitian–Einstein metrics for Higgs bundles over complete Hermitian manifolds’, Acta Math. Sci. 40(1) (2020), 211–225.CrossRefGoogle Scholar
Lubke, M. and Teleman, A., The Kobayashi–Hitchin Correspondence (World Scientific, Singapore, 1995).CrossRefGoogle Scholar
Mantegazza, C., ‘Smooth geometric evolutions of hypersurfaces’, Geom. Funct. Anal. 12(1) (2002), 138–182.CrossRefGoogle Scholar
Naito, H., ‘Finite time blowing-up for the Yang–Mills gradient flow in higher dimensions’, Hokkaido Math. J. 23(3) (1994), 451–464.CrossRefGoogle Scholar
Nie, Y.C. and Zhang, X., ‘The limiting behaviour of the Hermitian–Yang–Mills flow over compact non-Kähler manifolds’, Sci. China Math. 63 (2020), 1369–1390.CrossRefGoogle Scholar
Novaga, M. and Okabe, S., ‘Convergence to equilibrium of gradient flows defined on planar curves’, J. Reine Angew. Math. 2017(733) (2017), 87–119.CrossRefGoogle Scholar
Petrache, M. and Riviére, T., ‘The resolution of the Yang–Mills plateau problem in super-critical dimensions’, Adv. Math. 316 (2017), 469–540.CrossRefGoogle Scholar
Råde, J., ‘On the Yang–Mills heat equation in two and three dimensions’, J. reine angew. Math. 431 (1992), 123–163.Google Scholar
Saratchandran, H., ‘Higher order Seiberg–Witten functionals and their associated gradient flows’, Manuscripta Math. 160(3) (2019), 411–481.CrossRefGoogle Scholar
Schlatter, A. E., Struwe, M. and Tahvildar-Zadeh, A. S., ‘Global existence of the equivariant Yang–Mills heat flow in four space dimensions’, Amer. J. Math. 120(1) (1998), 117–128.Google Scholar
Sibley, B., ‘Asymptotics of the Yang–Mills flow for holomorphic vector bundles over Kähler manifolds: the canonical structure of the limit’, J. reine angew. Math. 706 (2015), 123–191.Google Scholar
Simonett, G., ‘The Willmore flow near spheres’, Differential Integral Equations 14(8) (2001), 1005–1014.Google Scholar
Simpson, C. T., ‘Constructing variations of Hodge structure using Yang–Mills theory and applications to uniformization’, J. Amer. Math. Soc. 1 (1988), 867–918.CrossRefGoogle Scholar
Song, C. and Wang, C., ‘Heat flow of Yang–Mills–Higgs functionals in dimension two’, J. Funct. Anal. 272(11) (2017), 4709–4751.CrossRefGoogle Scholar
Streets, J. D., ‘The gradient flow of ${\int}_m{\left| rm\right|}^2$ ’, J. Geom. Anal. 18(1) (2008), 249–271.CrossRefGoogle Scholar
Struwe, M., ‘On the evolution of harmonic mappings of Riemannian surfaces’, Comment. Math. Helv. 60(1) (1985), 558–581.CrossRefGoogle Scholar
Struwe, M., ‘The Yang–Mills flow in four dimensions’, Calc. Var. Partial Differential Equations 2(2) (1994), 123–150.CrossRefGoogle Scholar
Tao, T. and Tian, G., ‘A singularity removal theorem for Yang–Mills fields in higher dimensions’, J. Amer. Math. Soc. 17(3) (2004), 557–593.CrossRefGoogle Scholar
Trautwein, S., ‘Convergence of the Yang–Mills–Higgs flow on gauged holomorphic maps and applications’, Int. J. Math. 29(4) (2018), 1850024.CrossRefGoogle Scholar
Uhlenbeck, K. K., ‘Connections with ${l}^p$ -bounds on curvature’, Comm. Math. Phys. 83(1) (1982), 31–42.CrossRefGoogle Scholar
Uhlenbeck, K. K. and Yau, S. T., ‘On the existence of Hermitian–Yang–Mills connections in stable vector bundles’, Comm. Pure Appl. Math. 39(S1) (1986), S257–S293.CrossRefGoogle Scholar
Waldron, A., ‘Long-time existence for Yang–Mills flow’, Invent. Math. 217(3) (2019), 1069–1147.CrossRefGoogle Scholar
Wheeler, G., ‘Surface diffusion flow near spheres’, Calc. Var. Partial Differential Equations 44(1) (2012), 131–151.CrossRefGoogle Scholar
Wilkin, G., ‘Morse theory for the space of Higgs bundles’, Comm. Anal. Geom. 16 (2008), 283–332.CrossRefGoogle Scholar
Wilkin, G., ‘The reverse Yang–Mills–Higgs flow in a neighbourhood of a critical point’, J. Differential Geom. 115(1) (2020), 111–174.CrossRefGoogle Scholar
Zhang, C. J., Zhang, P. and Zhang, X., ‘Higgs bundles over non-compact Gauduchon manifolds’, Trans. Amer. Math. Soc. 74 (2021), 3735–3759.CrossRefGoogle Scholar