Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-26T07:31:37.159Z Has data issue: false hasContentIssue false
  • English
  • Français

Growth of solutions of weakly coupled parabolic systems and Laplace's equation

Part of: Higher-dimensional theory Partial differential equations Parabolic equations and systems Elliptic equations and systems

Published online by Cambridge University Press:  09 April 2009

N. A. Watson
N. A. Watson
Affiliation:
Department of Mathematics, University of Canterbury, Christchurch, New Zealand
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let ui(x, t) be the ith component of a nonnegative solution of a weakly coupled system of second-order, linear, parabolic partial differential equations, for x ∈ Rn and 0 < t < T. We obtain lower estimates, near t = 0, for the Lebesgue measure of the set of x for which 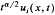exceeds 1. Related results for Poisson integrals on a half-space are also described, some applications are given, and interesting comparisons emerge.

MSC classification

Secondary: 35B05: Oscillation, zeros of solutions, mean value theorems, etc. 31B05: Harmonic, subharmonic, superharmonic functions 31B25: Boundary behavior 35B30: Dependence of solutions on initial and boundary data, parameters 35J05: Laplacian operator, reduced wave equation (Helmholtz equation), Poisson equation 35K45: Initial value problems for second-order parabolic systems
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 41 , Issue 3 , December 1986 , pp. 391 - 403
Copyright
Copyright © Australian Mathematical Society 1986

References

[1]Ahern, P., ‘The Poisson integral of a singular measure’, Canad. J. Math. 35 (1983), 735–749.CrossRefGoogle Scholar
[2]Armitage, D. H., ‘Normal limits, half-spherical means and boundary measures of half-space Poisson integrals’, Hiroshima Math. J. 11 (1981), 235–246.CrossRefGoogle Scholar
[3]Chabrowski, J. and Watson, N. A., ‘Properties of solutions of weakly coupled parabolic systems’, J. London Math. Soc. 23 (1981), 475–495.CrossRefGoogle Scholar
[4]Chabrowski, J., ‘Representation theorems for parabolic systems’, J. Austral. Math. Soc. Ser. A 32 (1982), 246–288.CrossRefGoogle Scholar
[5]Dinghas, A., ‘Über positive harmonische Funktionen in einem Halbraum’, Math. Z. 46 (1940), 559–570.CrossRefGoogle Scholar
[6]Flett, T. M., ‘On the rate of growth of mean values of holomorphic and harmonic functions’, Proc. London Math. Soc. 20 (1970), 749–768.CrossRefGoogle Scholar
[7]Gehring, F. W., ‘The Fatou theorem for functions harmonic in a half-space’, Proc. London Math. Soc. 8 (1958), 149–160.CrossRefGoogle Scholar
[8]Rogers, C. A. and Taylor, S. J., ‘Functions continuous and singular with respect to a Hausdorff measure’, Mathematika 8 (1961), 1–31.CrossRefGoogle Scholar