Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-27T10:42:52.110Z Has data issue: false hasContentIssue false
  • English
  • Français

Hall-closure and products of Fitting classes

Part of: Structure and classification of infinite or finite groups Representation theory of groups

Published online by Cambridge University Press:  09 April 2009

Owen J. Brison
Owen J. Brison
Affiliation:
Secção de Matemática Pura, Faculdade de Ciências, Avenida 24 de Julho, 134, 3°., 1.300 Lisboa, Portugal
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The Fitting class (of finite, soluble, groups), 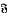, is said to be Hall π-closed (where π is a set of primes) if whenever G is a group in 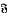and H is a Hall π-subgroup of G, then H belongs to 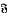. In this paper, we study the Hall π-closure of products of Fitting classes. Our main result is a characterisation of the Hall π-closedFitting classes of the form 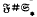(where 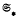denotes the so-called smallest normal Fitting class), subject to a restriction connecting π with the characteristic of 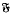. We also characterise those Fitting classes 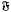(respectively, 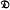) such that 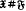(respectively, 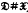) is Hall π-closed for all Fitting classes 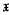. In each case, part of the proof uses a concrete group construction. As a bonus, one of these construction also yields a “cancellation result” for certain products of Fitting classes.

MSC classification

Secondary: 20D10: Solvable groups, theory of formations, Schunck classes, Fitting classes, $pi$-length, ranks 20D25: Special subgroups (Frattini, Fitting, etc.) 20E22: Extensions, wreath products, and other compositions
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 32 , Issue 2 , April 1982 , pp. 145 - 164
Copyright
Copyright © Australian Mathematical Society 1982

References

Beidleman, J. C. (1977), ‘On products and normal Fitting classes’, Arch. Math. (Basel) 28, 347–356.CrossRefGoogle Scholar
Berger, Thomas R. (1976), ‘More normal Fitting classes of finite solvable groups”, Math. Z. 151, 1–3.CrossRefGoogle Scholar
Dieter, Blessenohl und Wolfgang, Gaschütz (1970), ‘Über normale Schunck- und Fittingklassen’, Math. Z. 118, 1–8.Google Scholar
Owen, John Brison (1978), On the theory of Fitting classes of finite groups (Ph.D. thesis, University of Warwick).Google Scholar
Owen, J. Brison (1979), ‘Hall operators for Fitting classes’, Arch. Math. (Basel) 33, 1–9.Google Scholar
Bryant, R. M. and Kovacs, L. G. (1978), ‘Lie representations and groups of prime power order’, J. London Math. Soc. (2) 17, 415–421.CrossRefGoogle Scholar
Bryce, R. A. and John, Cossey (1974), ‘Metanilpotent Fitting classes’, J. Austral. Math. Soc. 17, 285–304.CrossRefGoogle Scholar
Bryce, R. A. and John, Cossey (1975), ‘A problem in the theory of normal Fitting classes’, Math. Z. 141, 99–110.CrossRefGoogle Scholar
John, Cossey (1975), ‘Products of Fitting classes’, Math. Z. 141, 289–295.Google Scholar
Elspeth, Cusack (1980), ‘Normal Fitting classes and Hall subgroups’, Bull. Austral. Math. Soc. 21, 229–236.Google Scholar
Terence, M. Gagen (1976), Topics in finite groups (London Mathematical Society Lecture Notes Series 16, Cambridge).Google Scholar
Hartley, B. (1969), ‘On Fischer's dualization of formation theory’, Proc. London Math. Soc. (3) 19, 193–207.CrossRefGoogle Scholar
Peter, Hauck (1978), ‘Eine Bemerkung zur kleinsten normalen Fittingklasse’, J. Algebra 53, 395–401.Google Scholar
Peter, Hauck (1979 a), ‘Fittingklassen und Kranzprodukte’, J. Algebra 59, 313–329.Google Scholar
Peter, Hauck (1979 b), ‘Onproducts of Fitting classes’, J. London Math. Soc. (2) 20, 423–434.Google Scholar
Huppert, B. (1967), Endliche Gruppen I (Springer-Verlag, Berlin, Heidleberg, New York).CrossRefGoogle Scholar
Hartmut, Laue, Hans, Lausch und GarryPain, R. (1977), ‘Verlagerung und normale Fittingklassen endlicher Gruppen’, Math. Z. 154, 257–260.Google Scholar
Lockett, F. P. (1971), On the theory of Fitting classes of finite soluble groups (Ph.D. thesis, University of Warwick).Google Scholar
Lockett, F. Peter (1974), ‘The Fitting class’ , Math. Z. 137, 131–136.CrossRefGoogle Scholar