Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Saloff-Coste, Laurent
and
Woess, Wolfgang
1996.
Computing Norms of Group-Invariant Transition Operators.
Combinatorics, Probability and Computing,
Vol. 5,
Issue. 2,
p.
161.
Saloff-Coste, Laurent
and
Woess, Wolfgang
1997.
Transition operators, groups, norms, and spectral radii.
Pacific Journal of Mathematics,
Vol. 180,
Issue. 2,
p.
333.
Mantero, A.M.
and
Zappa, Z.
1998.
The reduced group C*-algebra of a triangle building.
Bulletin of the Australian Mathematical Society,
Vol. 57,
Issue. 3,
p.
461.
Mantero, A. M.
and
Zappa, A.
2000.
Eigenfunctions of the Laplace operators for a building of type
$$\tilde A_2 $$
.
The Journal of Geometric Analysis,
Vol. 10,
Issue. 2,
Gérardin, P.
and
Lai, K.F.
2000.
Asymptotic behaviour of eigenfunctions on semi-homogeneous tree.
Pacific Journal of Mathematics,
Vol. 196,
Issue. 2,
p.
415.
Lindlbauer, Marc
and
Voit, Michael
2002.
Limit theorems for isotropic random walks on triangle buildings.
Journal of the Australian Mathematical Society,
Vol. 73,
Issue. 3,
p.
301.
Lubotzky, Alexander
Samuels, Beth
and
Vishne, Uzi
2005.
Ramanujan complexes of typeà d.
Israel Journal of Mathematics,
Vol. 149,
Issue. 1,
p.
267.
Heyer, Herbert
2006.
Wavelets, Multiscale Systems and Hypercomplex Analysis.
Vol. 167,
Issue. ,
p.
157.
Parkinson, James
2006.
Spherical harmonic analysis on affine buildings.
Mathematische Zeitschrift,
Vol. 253,
Issue. 3,
p.
571.
Parkinson, James
2006.
Buildings and Hecke algebras.
Journal of Algebra,
Vol. 297,
Issue. 1,
p.
1.
Kellil, Ferdaous
and
Rousseau, Guy
2008.
Opérateurs invariants sur certains immeubles affines de rang 2.
Annales de la Faculté des sciences de Toulouse : Mathématiques,
Vol. 16,
Issue. 3,
p.
591.
MANTERO, A. M.
and
ZAPPA, A.
2011.
AN EIGENSPACE OF LARGE DIMENSION FOR A HECKE ALGEBRA ON AN BUILDING.
Journal of the Australian Mathematical Society,
Vol. 91,
Issue. 1,
p.
29.
Mantero, A. M.
and
Zappa, A.
2014.
Macdonald formula for spherical functions on affine buildings.
Annales de la Faculté des sciences de Toulouse : Mathématiques,
Vol. 20,
Issue. 4,
p.
669.
Mantero, A. M.
and
Zappa, A.
2017.
Boundary behavior of generalized Poisson integrals on buildings of type $$\widetilde{A}_2$$ A ~ 2.
Bollettino dell'Unione Matematica Italiana,
Vol. 10,
Issue. 4,
p.
681.
Parkinson, James
2017.
Groups, Graphs and Random Walks.
p.
391.
Bader, Uri
Caprace, Pierre-Emmanuel
and
Lécureux, Jean
2018.
On the linearity of lattices in affine buildings and ergodicity of the singular Cartan flow.
Journal of the American Mathematical Society,
Vol. 32,
Issue. 2,
p.
491.
Hong, Soonki
and
Kwon, Sanghoon
2024.
Spectrum of the weighted adjacency operator on
a nonuniform arithmetic quotient of PGL3.
Combinatorics and Number Theory,
Vol. 13,
Issue. 2,
p.
103.
Hong, Soonki
and
Kwon, Sanghoon
2024.
Weak Ramanujan property of the standard non-uniform arithmetic quotient of PGL4.
International Journal of Number Theory,
Vol. 20,
Issue. 09,
p.
2355.
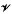 be its set of vertices. We study a commutative algebra
be its set of vertices. We study a commutative algebra 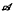 of ‘averaging’ operators acting on the space of complex valued functions on
of ‘averaging’ operators acting on the space of complex valued functions on 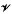 . This algebra may be identified with a space of ‘biradial functions’ on
. This algebra may be identified with a space of ‘biradial functions’ on 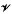 , or with a convolution algebra of bi-K-invariant functions on G, if G is a sufficiently large group of ‘type-rotating’ automorphisms of Δ, and K is the subgroup of G fixing a given vertex. We describe the multiplicative functionals on
, or with a convolution algebra of bi-K-invariant functions on G, if G is a sufficiently large group of ‘type-rotating’ automorphisms of Δ, and K is the subgroup of G fixing a given vertex. We describe the multiplicative functionals on 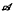 and the corresponding spherical functions. We consider the C*-algebra induced by
and the corresponding spherical functions. We consider the C*-algebra induced by 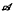 on l2
on l2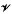 , find its spectrum Σ, prove positive definiteness of a kernel kz for each z ∈ Σ, find explicity the spherical Plancherel formula for any group G of type rotating automorphisms, and discuss the irreducibility of the unitary representations appearing therein. For the class of buildings ΔJ arising from the groups ΓJ introduced in [2], this involves proving that the weak closure of
, find its spectrum Σ, prove positive definiteness of a kernel kz for each z ∈ Σ, find explicity the spherical Plancherel formula for any group G of type rotating automorphisms, and discuss the irreducibility of the unitary representations appearing therein. For the class of buildings ΔJ arising from the groups ΓJ introduced in [2], this involves proving that the weak closure of 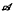 is maximal abelian in the von Neumann algebra generated by the left regular representation of ΓJ.
is maximal abelian in the von Neumann algebra generated by the left regular representation of ΓJ.