Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-27T11:20:57.976Z Has data issue: false hasContentIssue false
  • English
  • Français

Idempotent-generated regular semigroups

Published online by Cambridge University Press:  09 April 2009

C. Eberhart ,
W. Williams  and
L. Kinch
C. Eberhart
Affiliation:
University of KentuckyLexington, Kentucky 40506
W. Williams
Affiliation:
University of KentuckyLexington, Kentucky 40506
L. Kinch
Affiliation:
University of LouisvilleLouisville, Kentucky 40208 U.S.A.
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Suppose S is a regular semigroup and E is its set of idempotents. If E is subsemigroup of S, then S has been called orthodox and studied recently by Hall [3], Meakin [6], and Yamada [8]. In this paper we assume that E is not (necessarily) a subsemigroup of S and consider the subsemigroup generated by E, denoted <E>. If E denotes the set of all elements of S which can be written E, denoted <E>. If E denotes the set of all elements of S which can be written as the product of n (not necessarily distinct) idempotents of S, then . 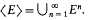We show that <E> is always a regular subsemigroup of S and investigate relationships between it and S. The case where <E> = S is of particular interest to us; such semigroups will be referred to as idempotent-generated regular semi- groups.

Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 15 , Issue 1 , February 1973 , pp. 27 - 34
Copyright
Copyright © Australian Mathematical Society 1973

References

[1]Anderson, L. W., Hunter, R. P., and Koch, R. J., ‘Some results on stability in semigroups’, Trans. Amer. Math. Soc., 117 (1965), 521–529.CrossRefGoogle Scholar
[2]Clifford, A. H. and Preston, G. B., The algebraic theory of semigroups, Vols I and II, Math. Surveys No. 7, (Providence, R. I., 1961 and 1967.)Google Scholar
[3]Erdös, J. A., ‘On products of idempotent matrices’, Glasgow Math. J., 8 (1967), 118–112.CrossRefGoogle Scholar
[4]Hall, T. E., ‘On regular semigroups whose idempotents form a subsemigroup’, Bull. Austral. Math. Soc., 1 (1969), 195–208.CrossRefGoogle Scholar
[5]Howie, J. M., ‘The subsemigroup generated by the idempotents of a full transformation semigroup’, J. London Math. Soc. 41 (1966), 707–716.CrossRefGoogle Scholar
[6]Howie, J. M. and Lallement, G., ‘Fundamental congruences on a regular semigroup’, Proc. Glasgow Math. Assoc., Vol. 7 (1966), 145–159.CrossRefGoogle Scholar
[7]Lallement, G., ‘Congurences et équivalences de Green sur un demi-groupe régulier’, C. R. Acad. Sci. Paris., Serie A, 262 (1966), 613–616.Google Scholar
[8]Meakin, J., ‘Congurences on orthodox semigroups’, J. Australian Math. Soc. 12 (1971) 323–341.CrossRefGoogle Scholar
[9]Petrich, M., ‘The maximal semilattice decomposition of a semigroup’, Math. Zeit. 85 (1964), 68–82.CrossRefGoogle Scholar
[10]Miyuki, Yamada, ‘On a regular semigroup in which the idempotents form a band’, Pacific J. Math. 33 (1970), 261–272.Google Scholar