Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Bambah, R. R.
Dumir, V. C.
and
Hans-Gill, R. J.
2000.
Number Theory.
p.
15.
Bambah, R. P.
Dumir, V. C.
and
Hans-Gill, R. J.
2000.
Number Theory.
p.
15.


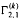 denote the
denote the 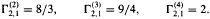
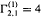 is already known. For non-zero forms it is proved that
is already known. For non-zero forms it is proved that 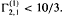 .
.