Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Izuchi, Keiji
and
Ohno, Sh�ichi
1997.
Selfadjoint commutators and invariant subspaces on the torus II.
Integral Equations and Operator Theory,
Vol. 27,
Issue. 2,
p.
208.
Ji, Guoxing
Ohwada, Tomoyoshi
and
Saito, Kichi-Suke
1998.
Certain invariant subspace structure of 𝐿²(𝕋²).
Proceedings of the American Mathematical Society,
Vol. 126,
Issue. 8,
p.
2361.
SETO, Michio
2005.
Submodules of $L^2(\mathbf{R}^2)$.
Tokyo Journal of Mathematics,
Vol. 28,
Issue. 2,
Izuchi, Keiji
and
Izuchi, Kou Hei
2006.
Rank-one commutators on invariant subspaces of the Hardy space on the bidisk.
Journal of Mathematical Analysis and Applications,
Vol. 316,
Issue. 1,
p.
1.
Izuchi, Kei Ji
Izuchi, Kou Hei
and
Izuchi, Yuko
2018.
Ranks of Cross-Commutators and Unitary Module Maps.
Computational Methods and Function Theory,
Vol. 18,
Issue. 3,
p.
545.

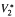 , For example, M is studied when the commutator is self-adjoint or of finite rank.
, For example, M is studied when the commutator is self-adjoint or of finite rank.