Hostname: page-component-78c5997874-fbnjt Total loading time: 0 Render date: 2024-11-14T17:33:53.940Z Has data issue: false hasContentIssue false
  • English
  • Français

Iterative criteria for bounds on the growth of positive solutions of a delay differential equation

Part of: Qualitative theory

Published online by Cambridge University Press:  09 April 2009

Raymond D. Terry
Raymond D. Terry
Affiliation:
California Polytechnic State University San Luis Obispo, California 93407U.S.A.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Following Terry (Pacific J. Math. 52 (1974), 269–282), the positive solutions of eauqtion (E): 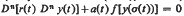are classified according to types Bj. We denote 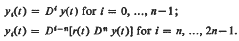A neccessary condition is given for a Bk-solution y(t) of (E) to satisfy y2k(t) ≥ m(t) > 0. In the case m(t) = C > 0, we obtain a sufficient condition for all solutions of (E) to be oscillatory.

MSC classification

Secondary: 34C10: Oscillation theory, zeros, disconjugacy and comparison theory 34C15: Nonlinear oscillations, coupled oscillators
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 25 , Issue 2 , March 1978 , pp. 195 - 200
Copyright
Copyright © Australian Mathematical Society 1978

References

REFERENCES

Burton, T. and Grimmer, R. (1972), “Oscillatory solutions of x″(t)+a(t)f[x(g(t))] = 0”, Delay and Functional Differential Equations and their Applications, 335–342 (Academic Press, New York).Google Scholar
Ladas, G. (1971), “On principal solutions of nonlinear differential equations”, J. Math. Anal. Appl. 36, 103–109.CrossRefGoogle Scholar
Terry, R. D. (1974), “Oscillatory properties of a delay differential equation of even order”, Pacific J. Math. 52, 269–282.CrossRefGoogle Scholar
Terry, R. D. (1975), “Some oscillation criteria for delay differential equations of even order”, SIAM J. Appl. Math. 28, 319–334.CrossRefGoogle Scholar
Terry, R. D. (1976), “Oscillatory and asymptotic properties of homogeneous and nonhomogeneous delay differential equations of even order”, J. Austral. Math. Soc. 22 (Ser. A), 282–304.CrossRefGoogle Scholar