Hostname: page-component-7bb8b95d7b-w7rtg Total loading time: 0 Render date: 2024-09-20T14:26:19.795Z Has data issue: false hasContentIssue false
  • English
  • Français

LEAVITT PATH ALGEBRAS OF WEIGHTED AND SEPARATED GRAPHS

Part of: Rings and algebras arising under various constructions

Published online by Cambridge University Press:  12 September 2022

PERE ARA
PERE ARA*
Affiliation:
Departament de Matemàtiques, Edifici Cc, Universitat Autònoma de Barcelona, 08193 Cerdanyola del Vallès (Barcelona), Spain and Centre de Recerca Matemàtica, Edifici Cc, Campus de Bellaterra, 08193 Cerdanyola del Vallès (Barcelona), Spain
*
e-mail: para@mat.uab.cat
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, we show that Leavitt path algebras of weighted graphs and Leavitt path algebras of separated graphs are intimately related. We prove that any Leavitt path algebra $L(E,\omega )$ of a row-finite vertex weighted graph 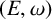$(E,\omega )$ is $*$-isomorphic to the lower Leavitt path algebra of a certain bipartite separated graph 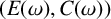$(E(\omega ),C(\omega ))$. For a general locally finite weighted graph $(E, \omega )$, we show that a certain quotient 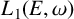$L_1(E,\omega )$ of 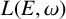$L(E,\omega )$ is $*$-isomorphic to an upper Leavitt path algebra of another bipartite separated graph 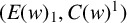$(E(w)_1,C(w)^1)$. We furthermore introduce the algebra 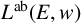${L^{\mathrm {ab}}} (E,w)$, which is a universal tame $*$-algebra generated by a set of partial isometries. We draw some consequences of our results for the structure of ideals of 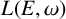$L(E,\omega )$, and we study in detail two different maximal ideals of the Leavitt algebra 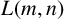$L(m,n)$.

Keywords

weighted graphseparated graphLeavitt path algebraideal

MSC classification

Secondary: 16S10: Rings determined by universal properties (free algebras, coproducts, adjunction of inverses, etc.)
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 115 , Issue 1 , August 2023 , pp. 1 - 25
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Communicated by Daniel Chan

Partially supported by DGI-MINECO-FEDER grant PID2020-113047GB-I00, and the Spanish State Research Agency, through the Severo Ochoa and María de Maeztu Program for Centers and Units of Excellence in R&D (CEX2020-001084-M).

References

Abrams, G., Ara, P. and Siles Molina, M., Leavitt Path Algebras, Lecture Notes in Mathematics, 2191 (Springer, London, 2017).CrossRefGoogle Scholar
Abrams, G. and Hazrat, R., ‘Connections between abelian sandpile models and the $K$ -theory of weighted Leavitt path algebras’, Preprint, 2022, arXiv:2112.09218v1 [math.RA].10.1007/s40879-023-00613-4CrossRefGoogle Scholar
Ara, P. and Cortiñas, G., ‘Tensor products of Leavitt path algebras’, Proc. Amer. Math. Soc. 141 (2013), 2629–2639.CrossRefGoogle Scholar
Ara, P. and Exel, R., ‘Dynamical systems associated to separated graphs, graph algebras, and paradoxical decompositions’, Adv. Math. 252 (2014), 748–804.CrossRefGoogle Scholar
Ara, P. and Facchini, A., ‘Direct sum decompositions of modules, almost trace ideals, and pullbacks of monoids’, Forum Math. 18 (2006), 365–389.CrossRefGoogle Scholar
Ara, P. and Goodearl, K. R., ‘Leavitt path algebras of separated graphs’, J. reine angew. Math. 669 (2012), 165–224.Google Scholar
Ara, P. and Lolk, M., ‘On the ideal structure of tame separated graph C*-algebras’, Adv. Math. 328 (2018), 367–435.10.1016/j.aim.2018.01.020CrossRefGoogle Scholar
Ara, P. and Perera, F., ‘Multipliers of von Neumann regular rings’, Comm. Algebra 28 (2000), 3359–3385.CrossRefGoogle Scholar
Bergman, G. M., ‘Coproducts and some universal ring constructions’, Trans. Amer. Math. Soc. 200 (1974), 33–88.CrossRefGoogle Scholar
Exel, R., Partial Dynamical Systems, Fell Bundles, and Applications, Mathematical Surveys and Monographs, 224 (American Mathematical Society, Providence, RI, 2017).CrossRefGoogle Scholar
Facchini, A. and Halter-Koch, F., ‘Projective modules and divisor homomorphisms ’, J. Algebra Appl. 2 (2003), 435–449.CrossRefGoogle Scholar
García, J. L. and Simón, J. J., ‘Morita equivalence for idempotent rings’, J. Pure Appl. Algebra 76 (1991), 39–56.CrossRefGoogle Scholar
Hazrat, R., ‘The graded structure of Leavitt path algebras’, Israel J. Math. 195 (2013), 833–895.CrossRefGoogle Scholar
Leavitt, W. G., ‘The module type of a ring’, Trans. Amer. Math. Soc. 103 (1962), 113–130.CrossRefGoogle Scholar
Preusser, R., ‘The V-monoid of a weighted Leavitt path algebra’, Israel J. Math. 234 (2019), 125–147.CrossRefGoogle Scholar
Preusser, R., ‘Weighted Leavitt path algebras—An overview’, Preprint, 2021, arXiv:2109.00434v1 [math.RA].Google Scholar
Sagan, B. E., The Symmetric Group: Representations, Combinatorial Algorithms, and Symmetric Functions, 2nd edn, Graduate Texts in Mathematics, 203 (Springer-Verlag, New York, 2001).CrossRefGoogle Scholar