Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-11T00:48:35.815Z Has data issue: false hasContentIssue false
  • English
  • Français

LIMITS OF HYPERCYCLIC AND SUPERCYCLIC OPERATOR MATRICES

Part of: General theory of linear operators

Published online by Cambridge University Press:  01 December 2008

XIAOHONG CAO
XIAOHONG CAO*
Affiliation:
College of Mathematics and Information Science, Shaanxi Normal University, Xi’an, 710062, People’s Republic of China (email: xiaohongcao@snnu.edu.cn)
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

An operator A on a complex, separable, infinite-dimensional Hilbert space H is hypercyclic if there is a vector x∈H such that the orbit {x,Ax,A2x,…} is dense in H. Using the character of the analytic core and quasinilpotent part of an operator A, we explore the hypercyclicity for upper triangular operator matrix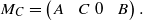

Keywords

hyperbolicityanalytic corequasi-nilpotent partspectrum

MSC classification

Secondary: 47A53: (Semi-) Fredholm operators; index theories 47A55: Perturbation theory 47A15: Invariant subspaces
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 85 , Issue 3 , December 2008 , pp. 367 - 376
Copyright
Copyright © Australian Mathematical Society 2009

References

[1]Aiena, P., Fredholm and Local Spectral Theory, with Applications to Multipliers (Kluwer Academic, Dordrecht, 2004).Google Scholar
[2]Cao, X., ‘Weyl type theorem and hypercyclicity II’, Proc. Amer. Math. Soc. 135 (2007), 1701–1708.Google Scholar
[3]Cao, X., ‘Weyl type theorem and hypercyclic operarors’, J. Math. Anal. Appl. 323 (2006), 267–274.CrossRefGoogle Scholar
[4]Cao, X. and Meng, B., ‘Essential approximate point spectrum and Weyl’s theorem for operator matrices’, J. Math. Anal. Appl. 304 (2005), 759–771.CrossRefGoogle Scholar
[5]Cao, X., ‘Browder essential approximate point spectrum and hypercyclicity for operator matrices’, Linear Algebra Appl. 426 (2007), 317–324.Google Scholar
[6]Colojoară, I. and Foiaş, C., Theory of Generalized Spectral Operators (Gordon and Breach, New York, 1968).Google Scholar
[7]Duggal, D. P. and Djordjević, S. V., ‘Dunford’s property and Weyl’s theorem’, Integral Equations Operator Theory 43 (2002), 290–297.Google Scholar
[8]Duggal, D. P., ‘Polaroid operators satisfying Weyl’s theorem’, Linear Algebra Appl. 414 (2006), 271–277.Google Scholar
[9]Finch, J. K., ‘The single valued extension property on a Banach space’, Pacific J. Math. 58 (1975), 61–69.Google Scholar
[10]Grabiner, S., ‘Uniform ascent and descent of bounded operators’, J. Math. Soc. Japan 34(2) (1982), 317–337.CrossRefGoogle Scholar
[11]Han, Y. M. and Kim, A. H., ‘A note on *-paranormal operators’, Integral Equations Operator Theory 49 (2004), 435–444.Google Scholar
[12]Herrero, D. A., ‘Limits of hypercyclic and supercyclic operators’, J. Funct. Anal. 99 (1991), 179–190.Google Scholar
[13]Hilden, H. M. and Wallen, L. J., ‘Some cyclic and non-cyclic vectors for certain operators’, Indiana Univ. Math. J. 23 (1974), 557–565.Google Scholar
[14]Kitai, C., ‘Invariant closed sets for linear operators’, Dissertation, University of Toronto, 1982.Google Scholar
[15]Mbekhta, M., ‘Généralisation de la décomposition de Kato aux opérateurs paranormaux et spectraux’, Glasgow Math. J. 29 (1987), 159–175.Google Scholar
[16]Mbekhta, M. and Ouahab, A., ‘Opérateurs s-regulier dans un espace de Banach et théorie spectrale’, Acta Sci. Math. (Szeged) 59 (1994), 525–543.Google Scholar
[17]Schmoeger, C., ‘On isolated point of the spectrum of a bounded linear operator’, Proc. Amer. Math. Soc. 117 (1993), 715–719.CrossRefGoogle Scholar
[18]Schmoeger, C., ‘Ascent, descent and the Atkinson region in Banach algebras II’, Ricerche Mat. XLII (1993), 249–264.Google Scholar