Article contents
LOGARITHMIC COEFFICIENTS PROBLEMS IN FAMILIES RELATED TO STARLIKE AND CONVEX FUNCTIONS
Published online by Cambridge University Press: 11 March 2019
Abstract
Let 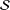 ${\mathcal{S}}$ be the family of analytic and univalent functions
${\mathcal{S}}$ be the family of analytic and univalent functions 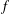 $f$ in the unit disk
$f$ in the unit disk  $\mathbb{D}$ with the normalization
$\mathbb{D}$ with the normalization 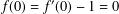 $f(0)=f^{\prime }(0)-1=0$, and let
$f(0)=f^{\prime }(0)-1=0$, and let 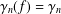 $\unicode[STIX]{x1D6FE}_{n}(f)=\unicode[STIX]{x1D6FE}_{n}$ denote the logarithmic coefficients of
$\unicode[STIX]{x1D6FE}_{n}(f)=\unicode[STIX]{x1D6FE}_{n}$ denote the logarithmic coefficients of 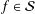 $f\in {\mathcal{S}}$. In this paper we study bounds for the logarithmic coefficients for certain subfamilies of univalent functions. Also, we consider the families
$f\in {\mathcal{S}}$. In this paper we study bounds for the logarithmic coefficients for certain subfamilies of univalent functions. Also, we consider the families 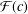 ${\mathcal{F}}(c)$ and
${\mathcal{F}}(c)$ and 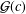 ${\mathcal{G}}(c)$ of functions
${\mathcal{G}}(c)$ of functions 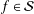 $f\in {\mathcal{S}}$ defined by
$f\in {\mathcal{S}}$ defined by 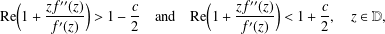 $$\begin{eqnarray}\text{Re}\biggl(1+{\displaystyle \frac{zf^{\prime \prime }(z)}{f^{\prime }(z)}}\biggr)>1-{\displaystyle \frac{c}{2}}\quad \text{and}\quad \text{Re}\biggl(1+{\displaystyle \frac{zf^{\prime \prime }(z)}{f^{\prime }(z)}}\biggr)<1+{\displaystyle \frac{c}{2}},\quad z\in \mathbb{D},\end{eqnarray}$$
$$\begin{eqnarray}\text{Re}\biggl(1+{\displaystyle \frac{zf^{\prime \prime }(z)}{f^{\prime }(z)}}\biggr)>1-{\displaystyle \frac{c}{2}}\quad \text{and}\quad \text{Re}\biggl(1+{\displaystyle \frac{zf^{\prime \prime }(z)}{f^{\prime }(z)}}\biggr)<1+{\displaystyle \frac{c}{2}},\quad z\in \mathbb{D},\end{eqnarray}$$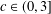 $c\in (0,3]$ and
$c\in (0,3]$ and 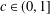 $c\in (0,1]$, respectively. We obtain the sharp upper bound for
$c\in (0,1]$, respectively. We obtain the sharp upper bound for 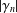 $|\unicode[STIX]{x1D6FE}_{n}|$ when
$|\unicode[STIX]{x1D6FE}_{n}|$ when 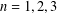 $n=1,2,3$ and
$n=1,2,3$ and 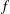 $f$ belongs to the classes
$f$ belongs to the classes 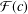 ${\mathcal{F}}(c)$ and
${\mathcal{F}}(c)$ and 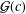 ${\mathcal{G}}(c)$, respectively. The paper concludes with the following two conjectures:
${\mathcal{G}}(c)$, respectively. The paper concludes with the following two conjectures:
∙ If
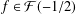 $f\in {\mathcal{F}}(-1/2)$, then
$f\in {\mathcal{F}}(-1/2)$, then 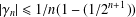 $|\unicode[STIX]{x1D6FE}_{n}|\leq 1/n(1-(1/2^{n+1}))$ for
$|\unicode[STIX]{x1D6FE}_{n}|\leq 1/n(1-(1/2^{n+1}))$ for 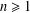 $n\geq 1$, and where
$n\geq 1$, and where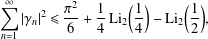 $$\begin{eqnarray}\mathop{\sum }_{n=1}^{\infty }|\unicode[STIX]{x1D6FE}_{n}|^{2}\leq {\displaystyle \frac{\unicode[STIX]{x1D70B}^{2}}{6}}+{\displaystyle \frac{1}{4}}~\text{Li}_{2}\biggl({\displaystyle \frac{1}{4}}\biggr)-\text{Li}_{2}\biggl({\displaystyle \frac{1}{2}}\biggr),\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{n=1}^{\infty }|\unicode[STIX]{x1D6FE}_{n}|^{2}\leq {\displaystyle \frac{\unicode[STIX]{x1D70B}^{2}}{6}}+{\displaystyle \frac{1}{4}}~\text{Li}_{2}\biggl({\displaystyle \frac{1}{4}}\biggr)-\text{Li}_{2}\biggl({\displaystyle \frac{1}{2}}\biggr),\end{eqnarray}$$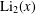 $\text{Li}_{2}(x)$ denotes the dilogarithm function.
$\text{Li}_{2}(x)$ denotes the dilogarithm function.∙ If
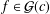 $f\in {\mathcal{G}}(c)$, then
$f\in {\mathcal{G}}(c)$, then 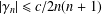 $|\unicode[STIX]{x1D6FE}_{n}|\leq c/2n(n+1)$ for
$|\unicode[STIX]{x1D6FE}_{n}|\leq c/2n(n+1)$ for 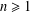 $n\geq 1$.
$n\geq 1$.
MSC classification
Information
- Type
- Research Article
- Information
- Journal of the Australian Mathematical Society , Volume 109 , Issue 2 , October 2020 , pp. 230 - 249
- Copyright
- © 2019 Australian Mathematical Publishing Association Inc.
Footnotes
The work of the first author is supported by Mathematical Research Impact Centric Support of Department of Science and Technology (DST), India (MTR/2017/000367). The second author thanks the Science and Engineering Research Board, DST, India, for its support by SERB National Post-Doctoral Fellowship (grant no. PDF/2016/001274).
References
- 31
- Cited by


