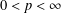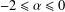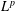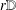Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Wang, Chunjie
and
Xiao, Jie
2016.
Addendum to “Gaussian Integral Means of Entire Functions”.
Complex Analysis and Operator Theory,
Vol. 10,
Issue. 3,
p.
495.
Ferguson, Timothy
2017.
Bergman–Hölder Functions, Area Integral Means and Extremal Problems.
Integral Equations and Operator Theory,
Vol. 87,
Issue. 4,
p.
545.
Peng, Weiqiang
Wang, Chunjie
and
Zhu, Kehe
2017.
Convexity of area integral means for analytic functions.
Complex Variables and Elliptic Equations,
Vol. 62,
Issue. 3,
p.
307.
DOUBTSOV, EVGUENI
2018.
INTEGRAL MEANS OF HOLOMORPHIC FUNCTIONS AS GENERIC LOG-CONVEX WEIGHTS.
Bulletin of the Australian Mathematical Society,
Vol. 97,
Issue. 1,
p.
88.
Wang, Chunjie
and
Yang, Wenjie
2019.
Area integral means over the annuli.
Journal of Mathematical Analysis and Applications,
Vol. 473,
Issue. 1,
p.
510.
Hu, Qinxia
and
Wang, Chunjie
2020.
Convexity for area integral means.
Journal of Mathematical Analysis and Applications,
Vol. 491,
Issue. 2,
p.
124345.
段, 玉聪
2022.
Logarithmic Convexity of Area Integral Means.
Pure Mathematics,
Vol. 12,
Issue. 05,
p.
749.