Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Dvurečenskij, Anatolij
and
Zahiri, Omid
2019.
States on EMV-algebras.
Soft Computing,
Vol. 23,
Issue. 17,
p.
7513.
Dvurečenskij, Anatolij
and
Zahiri, Omid
2019.
Generalized pseudo-EMV-effect algebras.
Soft Computing,
Vol. 23,
Issue. 20,
p.
9807.
Borzooei, R. A.
Shenavaei, M.
Di Nola, A.
and
Zahiri, O.
2019.
On EMV-Semirings.
Mathematica Slovaca,
Vol. 69,
Issue. 4,
p.
739.
Borzooei, R. A.
Shenavaei, M.
Di Nola, A.
and
Zahiri, O.
2020.
Ideals of an EMV-semiring.
International Journal of General Systems,
Vol. 49,
Issue. 3,
p.
235.
Dvurečenskij, Anatolij
and
Zahiri, Omid
2021.
A variety containing EMV-algebras and Pierce sheaves of EMV-algebras.
Fuzzy Sets and Systems,
Vol. 418,
Issue. ,
p.
101.
Dvurečenskij, Anatolij
and
Zahiri, Omid
2021.
Algebraic Perspectives on Substructural Logics.
Vol. 55,
Issue. ,
p.
107.
Dvurečenskij, Anatolij
and
Zahiri, Omid
2021.
Locally $$\sigma $$-complete and locally complete EMV-algebras.
Soft Computing,
Vol. 25,
Issue. 2,
p.
883.
Dvurečenskij, Anatolij
and
Zahiri, Omid
2022.
Pierce sheaves of pseudo EMV-algebras.
Soft Computing,
Vol. 26,
Issue. 17,
p.
8351.
Liu, Hongxing
2022.
On topology of maximal ideals of EBL-algebras.
Soft Computing,
Vol. 26,
Issue. 10,
p.
4541.
Dvurečenskij, Anatolij
and
Zahiri, Omid
2023.
On EMV-algebras with square roots.
Journal of Mathematical Analysis and Applications,
Vol. 524,
Issue. 2,
p.
127113.
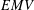 $EMV$-ALGEBRAS
$EMV$-ALGEBRAS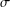 $\unicode[STIX]{x1D70E}$-complete
$\unicode[STIX]{x1D70E}$-complete 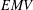 $EMV$-algebras, we prove an analogue of the Loomis–Sikorski theorem showing that every
$EMV$-algebras, we prove an analogue of the Loomis–Sikorski theorem showing that every 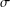 $\unicode[STIX]{x1D70E}$-complete
$\unicode[STIX]{x1D70E}$-complete 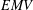 $EMV$-algebra is a
$EMV$-algebra is a 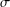 $\unicode[STIX]{x1D70E}$-homomorphic image of an
$\unicode[STIX]{x1D70E}$-homomorphic image of an 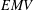 $EMV$-tribe of fuzzy sets where all algebraic operations are defined by points. To prove it, some topological properties of the state-morphism space and the space of maximal ideals are established.
$EMV$-tribe of fuzzy sets where all algebraic operations are defined by points. To prove it, some topological properties of the state-morphism space and the space of maximal ideals are established.