Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-14T17:43:04.124Z Has data issue: false hasContentIssue false
  • English
  • Français

Mal'tsev conditions and spectra

Part of: Varieties

Published online by Cambridge University Press:  09 April 2009

Walter Taylor
Walter Taylor
Affiliation:
Department of Mathematics University of ColoradoBoulder, Colorado 80309, USA
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let J be a cofinite set of positive integers which contains 1. In (1973) I proved that the following condition on a variety (equational class) 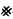is Mal'tsev-definable: if υ ∈and υ is finite, then |υ| ∈J. This article contains some subsidiary results, concerned mainly with a more detailed description of these Mal'tsev conditions. Many of our results arose upon considering a recent article of W. D. Neumann (1978).

MSC classification

Secondary: 08B05: Equational logic, Mal′cev (Mal′tsev) conditions
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 29 , Issue 2 , March 1980 , pp. 143 - 152
Copyright
Copyright © Australian Mathematical Society 1980

References

Baker, K. (1977), ‘Finite equational bases for finite algebras in a congruence-distributive equational class’, Advances in Math. 24, 207–243.CrossRefGoogle Scholar
Baldwin, J. T. and Berman, J. (1977), ‘A model-theoretic approach to Malcev conditions’, J. Symbolic Logic 42, 277–288.CrossRefGoogle Scholar
Birkhoff, G. (1967), Lattice theory 3rd ed. (Amer. Math. Soc. Colloq. Publications, 25, New York).Google Scholar
Biryukov, A. P. (1965), ‘On infinite sets of identities in semigroups’, Algebra i Logika 4, 31–32.Google Scholar
Bulman-Fleming, S. and Taylor, W. (1976), ‘Union-indecomposable varieties’, Colloq. Math. 35, 189–199.Google Scholar
Chang, C. C. and Keisler, H. J. (1973), Model Theory (Studies in Logic and the Foundations of Mathematics, 73, North-Holland, Amsterdam, 1973).Google Scholar
Cohn, P. M. (1965), Universal Algebra (Harper's Series in Modern Mathematics, Harper and Row, New York, 1965).Google Scholar
Evans, T. (1968), ‘The number of semigroup varieties’, Quart. J. Math. (Oxford) (2) 19, 335–336.CrossRefGoogle Scholar
Freyd, P. (1966), ‘Algebra valued functors in general, and tensor products in particular’, Colloq. Math. 14, 89–106.CrossRefGoogle Scholar
Grätzer, G. (1968), Universal algebra (The University Series in Higher Mathematics, Van Nostrand, Princeton, 1968).Google Scholar
Isbell, J. R. (1970), ‘Two examples in varieties of monoids’, Proc. Cambridge Phios. Soc. 68, 265–266.Google Scholar
Jónsson, B., McNulty, G. and Quackenbush, R. W. (1975), ‘The ascending and descending varietal chains of a variety’, Canad. J. Math. 27, 25–32.Google Scholar
McKenzie, R. (1975), ‘On spectra, and the negative solution of the decision problem for identities having a finite non-trivial model’, J. Symbolic Logic 40, 186–196.Google Scholar
Neumann, W. D. (1974), ‘On Malcev conditions’, J. Austral. Math. Soc. 17, 376–384.CrossRefGoogle Scholar
Neumann, W. D. (1978), ‘Mal'cev conditions, spectra and Kronecker products’, J. Austral. Math. Soc. Ser. A 25, 103–117.CrossRefGoogle Scholar
Padmanabhan, R. and Quackenbush, R. W. (1973), ‘Equational theories of algebras with distributive congruences’, Proc. Amer. Math. Soc. 41, 373–377.CrossRefGoogle Scholar
Quackenbush, R. W. (1979), ‘Primal algebras’, an appendix to the forthcoming new edition of Grätzer, G. (1968) (to appear).Google Scholar
Taylor, W. (1972), ‘Fixed points of endomorphisms’, Algebra Universalis 2, 74–76.Google Scholar
Taylor, W. (1973), ‘Characterizing Mal'cev conditions’, Algebra Universalis 3, 351–397.CrossRefGoogle Scholar
Taylor, W. (1974), ‘Uniformity of congruences’, Algebra Universalis 4, 342–360.Google Scholar
Taylor, W. (1975), ‘The fine spectrum of a variety’, Algebra Universalis 5, 263–303.CrossRefGoogle Scholar
Taylor, W. (1978), ‘Miscellaneous results on Mal'tsev conditions’, Notices Amer. Math. Soc. 25, A-581.Google Scholar
Taylor, W. (1979), review of Neumann, W. D. (1978), MR., 58 449.Google Scholar
Taylor, W. (1979a), ‘Equational logic’, Houston J. Math. Survey volume 1979, iii + 83 pp. An abridgement is to appear in the forthcoming new edition of Grätzer, G. (1968).Google Scholar
Vaughan-Lee, M. R. (1970), ‘Uncountably many varieties of groups’, Bull. London Math. Soc. 2, 280–286.CrossRefGoogle Scholar