Hostname: page-component-78c5997874-fbnjt Total loading time: 0 Render date: 2024-11-10T19:58:47.593Z Has data issue: false hasContentIssue false
  • English
  • Français

Maximum principles for parabolic equations

Part of: Partial differential equations

Published online by Cambridge University Press:  09 April 2009

Giovanni Porru  and
Salvatore Serra
Giovanni Porru
Affiliation:
Dipartimento di Matematica, Universita degli studi di Cagliari, Via Ospedale 72, 09124 Cagliari, Italy
Salvatore Serra
Affiliation:
Dipartimento di Matematica, Universita degli studi di Cagliari, Via Ospedale 72, 09124 Cagliari, Italy
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let u(x, t) be a smooth function in the domain Q = Ω × (0, L), Ω in 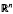n, let Du be the spatial gradient of u(x, t) and let ∇u = (Du, u1). If u(x, t) satisfies the parabolic equation F(u, Du, D2u) = ut, we define w(x, t) by g(w) = │∇u│−1G(∇u) (g is positive and decreasing, G is concave and homogeneous of degree one) and we prove that w(x, t) attains its maximum value on the parabolic boundary of Q. If u(x, t) satisfies the equation Δu + 2h(q2) uiujuij = ut(q2 = │Du│2, 1 + 2q2h(q2) > 0) we prove that qf (u) takes its maximum value on the parabolic boundary of Q provided f satisfies a suitable condition. If u(x, t) satisfies the parabolic equation aij (Du)uij − b(x, t, u, Du) = ut (b is concave with respect to (x, t, u)) we define C(x, y, t, τ) = u(z, θ) − αu(x, t) − βu(y, τ) (0 < α, 0 < β, α + β = 1, z αx +y, θ = αt + βτ) and we prove that if C(x, y, t, r) ≤0 when x, y, z ∈ Ω2 and one of t, τ = 0, and when t, τ ∈ (0, L], and one of x, y, z, ∈ ∂Ω, then it is C(x, y, t, τ) ≤0 everywhere.

MSC classification

Secondary: 35B50: Maximum principles
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 56 , Issue 1 , February 1994 , pp. 41 - 52
Copyright
Copyright © Australian Mathematical Society 1994

References

[1]Buttu, A., ‘An angle's maximum principle for the gradient of solutions of parabolic equations’, Boll. Un. Mat. Ital. A 2 (1988), 405–408.Google Scholar
[2]Haraux, A., Nonlinear evolution equations-global behaviour of solutions, Lecture Notes in Math. 841 (Springer, Berlin, 1981).CrossRefGoogle Scholar
[3]Henry, D., Geometric theory of semilinear parabolic equations, Lecture Notes in Math. 840 (Springer, Berlin, 1981).CrossRefGoogle Scholar
[4]Kawohl, B., Rearrangements and convexity of level sets in PDE, Lecture Notes in Math. 1150 (Springer, Berlin, 1985).CrossRefGoogle Scholar
[5]Korevaar, N., ‘Capillarity surface convexity above convex domains’, Indiana Univ. Math. J. 32 (1983), 73–82.CrossRefGoogle Scholar
[6]Korevaar, N., ‘Convex solutions to nonlinear elliptic and parabolic boundary value problems’, Indiana Univ. Math. J. 32 (1983), 603–614.CrossRefGoogle Scholar
[7]Payne, L. P. and Philippin, G. A., ‘On some maximum principles involving harmonic functions and their derivatives’, SIAM J. Math. Anal. 10 (1979), 96–104.CrossRefGoogle Scholar
[8]Philippin, G. A., ‘On a free boundary problem in electrostatic’, Math. Methods Appl. Sci. 12 (1990), 387–392.CrossRefGoogle Scholar
[9]Philippin, G. A. and Payne, L. P., ‘On the conformal capacity problem’, Sympos. Math. 30 (1989), 119–136.Google Scholar
[10]Porru, G. and Ragnedda, F., ‘Convexity properties for solutions of some second order elliptic semilinear equations’, Appi. Anal. 37 (1990), 1–18.CrossRefGoogle Scholar
[11]Protter, M. H. and Weinberger, H. F., Maximum principles in differential equations (PrenticeHall, Englewood Cuffs, 1967).Google Scholar
[12]Pucci, C., ‘An angle's maximum principle for the gradient of solutions of elliptic equations’, Boll. Un. Mat. Ital. A 1 (1987), 135–139.Google Scholar
[13]>Pucci, C., ‘A maximum principle related to level surfaces of solutions of parabolic equations’, J. Austral. Math. Soc. (Series A) 46 (1989), 1–7.CrossRefGoogle Scholar