Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-26T08:46:57.607Z Has data issue: false hasContentIssue false
  • English
  • Français

M-Cohyponormal powers of composition operators

Part of: Special classes of linear operators

Published online by Cambridge University Press:  09 April 2009

Satish K. Khurana  and
Babu Ram
Satish K. Khurana
Affiliation:
Maharshi Dayanand UniversityRohtak -124001, India
Babu Ram
Affiliation:
Maharshi Dayanand UniversityRohtak -124001, India
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

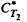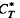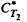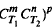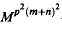Let T1, i = 1, 2 be measurable transformations which define bounded composition operators C Ti on L2 of a σ-finite measure space. Let us denote the Radon-Nikodym derivative of with respect to m by hi, i = 1, 2. The main result of this paper is that if and are both M-hyponormal with h1 ≤ M2(h2 o T2) a.e. and h2 ≤ M2(h1 o T1) a.e., then for all positive integers m, n and p, []* is -hyponormal. 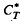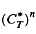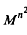As a consequence, we see that if is an M-hyponormal composition operator, then is -hyponormal for all positive integers n.

MSC classification

Secondary: 47B20: Subnormal operators, hyponormal operators, etc. 47B38: Operators on function spaces (general)
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 53 , Issue 1 , August 1992 , pp. 9 - 16
Copyright
Copyright © Australian Mathematical Society 1992

References

[1]Harrington, D. J. and Whitley, R., ‘Seminormal composition operators’, J. Operator Theory 11 (1984), 125–135.Google Scholar
[2]Dibrell, P. and Campbell, J. T., ‘Hyponormal powers of composition operators’, Proc. Amer. Math. Soc. 102 (4) (1988), 914–18.CrossRefGoogle Scholar
[3]Halmos, P. R., A Hilbert space problem book (Van Nostrand, Princeton, N.J., 1976).Google Scholar