No CrossRef data available.
Article contents
Natural extensions of probability measure in function space
Published online by Cambridge University Press: 09 April 2009
Extract
Let {Xt}t ∈ T be a family of real (R) random variable defined on a probability space (Ω, A P) and having the ranges in a subset S of R, that is, Xt (Ω) ⊂ S for all t. Let X be the mapping of Ω into the function space St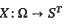 such that for any ω ∈ Ω
such that for any ω ∈ Ω 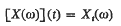 We shall write X = {Xt}t ∈ T and call X the random fundtion arising from {Xt}t ∈ T. It is well-known that any finite subfamily of {Xt}t∈T induces a “finite joint distribution” in ST, and according to Kolmogorov (1933) these finite joint distributions can be simultaneously extended to a probability measure Po on the Borel class Bo of subsets of ST. This extension is natural in the sense that for any B∈B0P0(B) turns out to be exactly P[X−1(B)]. The Kolmogorov extension Po has however a shortcoming in that its domain B0 is not broad enough to include many events of practical interest.
We shall write X = {Xt}t ∈ T and call X the random fundtion arising from {Xt}t ∈ T. It is well-known that any finite subfamily of {Xt}t∈T induces a “finite joint distribution” in ST, and according to Kolmogorov (1933) these finite joint distributions can be simultaneously extended to a probability measure Po on the Borel class Bo of subsets of ST. This extension is natural in the sense that for any B∈B0P0(B) turns out to be exactly P[X−1(B)]. The Kolmogorov extension Po has however a shortcoming in that its domain B0 is not broad enough to include many events of practical interest.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Australian Mathematical Society 1975

