Hostname: page-component-78c5997874-4rdpn Total loading time: 0 Render date: 2024-11-10T13:23:25.876Z Has data issue: false hasContentIssue false
  • English
  • Français

A NEURAL NETWORK FOR THE GENERALIZED NONLINEAR COMPLEMENTARITY PROBLEM OVER A POLYHEDRAL CONE

Published online by Cambridge University Press:  30 October 2015

YIFEN KE  and
CHANGFENG MA
YIFEN KE
Affiliation:
School of Mathematics and Computer Science, Fujian Normal University, Fuzhou 350117, PR China email yfke89@163.com
CHANGFENG MA*
Affiliation:
School of Mathematics and Computer Science, Fujian Normal University, Fuzhou 350117, PR China email macf@fjnu.edu.cn
*
✉macf@fjnu.edu.cn
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper, we consider a neural network model for solving the generalized nonlinear complementarity problem (denoted by GNCP) over a polyhedral cone. The neural network is derived from an equivalent unconstrained minimization reformulation of the GNCP, which is based on the penalized Fischer–Burmeister function 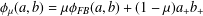${\it\phi}_{{\it\mu}}(a,b)={\it\mu}{\it\phi}_{\mathit{FB}}(a,b)+(1-{\it\mu})a_{+}b_{+}$. We establish the existence and the convergence of the trajectory of the neural network, and study its Lyapunov stability, asymptotic stability and exponential stability. It is found that a larger 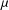${\it\mu}$ leads to a better convergence rate of the trajectory. Simulation results are also reported.

Keywords

generalized nonlinear complementarity problempolyhedral coneneural networkconvergence analysissimulation results

MSC classification

Primary: 90C33: Complementarity and equilibrium problems and variational inequalities (finite dimensions)
Secondary: 65K10: Optimization and variational techniques
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 99 , Issue 3 , December 2015 , pp. 364 - 379
Copyright
© 2015 Australian Mathematical Publishing Association Inc. 

References

Bouzerdoum, A. and Pattison, T. R., ‘Neural network for quadratic optimization with bound constraints’, IEEE Trans. Neural Netw. 4 (1993), 293–304.CrossRefGoogle ScholarPubMed
Chen, B.-T., Chen, X.-J. and Kanzow, C., ‘A penalized Fischer–Burmeister NCP-function: theoretical investigation and numerical results’, Math. Program. 88(1) (1997), 211–216.CrossRefGoogle Scholar
Chen, X.-H and Ma, C.-F., ‘A regularization smoothing Newton method for solving nonlinear complementarity problem’, Nonlinear Anal. Real World Appl. 10 (2009), 1702–1711.CrossRefGoogle Scholar
Chen, B.-L. and Ma, C.-F., ‘Superlinear/quadratic smoothing Broyden-like method for the generalized nonlinear complementarity problem’, Nonlinear Anal. Real World Appl. 12 (2011), 1250–1263.CrossRefGoogle Scholar
Chen, J.-S., Ko, C. H. and Pan, S. H., ‘A neural network based on the generalized Fischer–Burmeister function for nonlinear complementarity problems’, Inform. Sci. 180 (2010), 697–711.CrossRefGoogle Scholar
Hopfield, J. J. and Tank, D. W., ‘Neural computation of decision in optimization problems’, Biol. Cybernet. 52 (1985), 141–152.CrossRefGoogle ScholarPubMed
Kojima, M. and Shindo, S., ‘Extensions of Newton and quasi-Newton methods to systems of PC1 equations’, J. Oper. Res. Soc. Japan 29 (1986), 352–374.Google Scholar
Liao, L.-Z. and Qi, H.-D., ‘A neural network for the linear complementarity problem’, Math. Comput. Model. 29 (1999), 9–18.Google Scholar
Liao, L.-Z., Qi, H.-D. and Qi, L., ‘Solving nonlinear complementarity problems with neural networks: a reformulation method approach’, J. Comput. Appl. Math. 131 (2001), 342–359.CrossRefGoogle Scholar
Ma, C.-F., ‘A new smoothing and regularization Newton method for P 0 -NCP’, J. Global Optim. 48 (2010), 241–261.CrossRefGoogle Scholar
Ma, C.-F., Chen, L.-J. and Wang, D.-S., ‘A globally and superlinearly convergent smoothing Broyden-like method for solving nonlinear complementarity problem’, Appl. Math. Comput. 198 (2008), 592–604.Google Scholar
Ma, C.-F., Jiang, L.-H. and Wang, D.-S., ‘The convergence of a smoothing damped Gauss–Newton method for nonlinear complementarity problem’, Nonlinear Anal. Real World Appl. 10 (2009), 2072–2087.CrossRefGoogle Scholar
Tank, D. W. and Hopfield, J. J., ‘Simple neural optimization networks: an A/D converter, signal decision circuit, and a linear programming circuit’, IEEE Trans. Circuits Syst. I. Regul. Pap. 33 (1986), 533–541.CrossRefGoogle Scholar
Wang, Y.-J., Ma, F.-M. and Zhang, J.-Z., ‘A nonsmooth L-M method for solving the generalized nonlinear complementarity problem over a polyhedral cone’, Appl. Math. Optim. 52(1) (2005), 73–92.CrossRefGoogle Scholar
Xia, Y., Leung, H. and Wang, J., ‘A projection neural network and its application to constrained optimization problems’, IEEE Trans. Circuits Syst. I. Regul. Pap. 49 (2002), 447–458.Google Scholar
Zak, S. H., Upatising, V. and Hui, S., ‘Solving linear programming problems with neural networks: a comparative study’, IEEE Trans. Neural Netw. 6 (1995), 94–104.CrossRefGoogle ScholarPubMed