No CrossRef data available.
Article contents
NILPOTENT SUBSPACES AND NILPOTENT ORBITS
Published online by Cambridge University Press: 30 May 2018
Abstract
Let 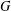 $G$ be a semisimple complex algebraic group with Lie algebra
$G$ be a semisimple complex algebraic group with Lie algebra 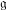 $\mathfrak{g}$. For a nilpotent
$\mathfrak{g}$. For a nilpotent 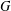 $G$-orbit
$G$-orbit 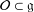 ${\mathcal{O}}\subset \mathfrak{g}$, let
${\mathcal{O}}\subset \mathfrak{g}$, let 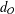 $d_{{\mathcal{O}}}$ denote the maximal dimension of a subspace
$d_{{\mathcal{O}}}$ denote the maximal dimension of a subspace 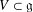 $V\subset \mathfrak{g}$ that is contained in the closure of
$V\subset \mathfrak{g}$ that is contained in the closure of 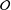 ${\mathcal{O}}$. In this note, we prove that
${\mathcal{O}}$. In this note, we prove that 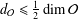 $d_{{\mathcal{O}}}\leq {\textstyle \frac{1}{2}}\dim {\mathcal{O}}$ and this upper bound is attained if and only if
$d_{{\mathcal{O}}}\leq {\textstyle \frac{1}{2}}\dim {\mathcal{O}}$ and this upper bound is attained if and only if 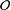 ${\mathcal{O}}$ is a Richardson orbit. Furthermore, if
${\mathcal{O}}$ is a Richardson orbit. Furthermore, if 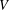 $V$ is
$V$ is 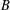 $B$-stable and
$B$-stable and 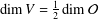 $\dim V={\textstyle \frac{1}{2}}\dim {\mathcal{O}}$, then
$\dim V={\textstyle \frac{1}{2}}\dim {\mathcal{O}}$, then 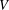 $V$ is the nilradical of a polarisation of
$V$ is the nilradical of a polarisation of 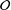 ${\mathcal{O}}$. Every nilpotent orbit closure has a distinguished
${\mathcal{O}}$. Every nilpotent orbit closure has a distinguished 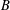 $B$-stable subspace constructed via an
$B$-stable subspace constructed via an 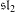 $\mathfrak{sl}_{2}$-triple, which is called the Dynkin ideal. We then characterise the nilpotent orbits
$\mathfrak{sl}_{2}$-triple, which is called the Dynkin ideal. We then characterise the nilpotent orbits 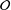 ${\mathcal{O}}$ such that the Dynkin ideal (1) has the minimal dimension among all
${\mathcal{O}}$ such that the Dynkin ideal (1) has the minimal dimension among all 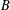 $B$-stable subspaces
$B$-stable subspaces  $\mathfrak{c}$ such that
$\mathfrak{c}$ such that 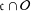 $\mathfrak{c}\cap {\mathcal{O}}$ is dense in
$\mathfrak{c}\cap {\mathcal{O}}$ is dense in  $\mathfrak{c}$, or (2) is the only
$\mathfrak{c}$, or (2) is the only 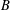 $B$-stable subspace
$B$-stable subspace  $\mathfrak{c}$ such that
$\mathfrak{c}$ such that 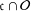 $\mathfrak{c}\cap {\mathcal{O}}$ is dense in
$\mathfrak{c}\cap {\mathcal{O}}$ is dense in  $\mathfrak{c}$.
$\mathfrak{c}$.
MSC classification
- Type
- Research Article
- Information
- Journal of the Australian Mathematical Society , Volume 106 , Issue 1 , February 2019 , pp. 104 - 126
- Copyright
- © 2018 Australian Mathematical Publishing Association Inc.
Footnotes
The research of the first author was carried out at the IITP R.A.S. at the expense of the Russian Foundation for Sciences (project no. 14-50-00150). The second author is partially supported by the DFG priority programme SPP 1388 ‘Darstellungstheorie’ and by the Graduiertenkolleg GRK 1523 ‘Quanten- und Gravitationsfelder’.


