Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-26T17:59:43.575Z Has data issue: false hasContentIssue false
  • English
  • Français

Normal characterization by zero correlations

Part of: Distribution theory - Probability Distribution theory

Published online by Cambridge University Press:  09 April 2009

Eugene Seneta  and
Gabor J. Szekely
Eugene Seneta
Affiliation:
School of Mathematics and Statistics University of SydneyNSW 2006Australia e-mail: eseneta@maths.usyd.edu.au
Gabor J. Szekely
Affiliation:
Department of Mathematics and Statistics Bowling Green State UniversityBowling Green OH 43403USA e-mail: gabors@bgnet.bgsu.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Suppose Xi, i = 1,…,n are indepedent and identically distributed with E/X1/r < ∞, r = 1,2,…. If Cov ((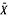 − μ)r, S2) = 0 for r = 1, 2,…, where μ = EX1, S2 = 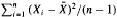, and 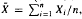, then we show X1 ~ N (μ, σ2), where σ2 = Var(X1). This covariance zero condition charaterizes the normal distribution. It is a moment analogue, by an elementary approach, of the classical characterization of the normal distribution by independence of 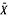and S2 using semi invariants. More generally, if Cov 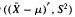= 0 for r = 1,…, k, then E((X1 − μ)/σ)r+2 = EZr+2 for r = 1,… k, where Z ~ N(0, 1). Conversely Corr 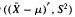may be arbitrarily close to unity in absolute value, but for unimodal X1, Corr2( < 15/16, and this bound is the best possible.

MSC classification

Secondary: 60E05: Distributions 62E10: Characterization and structure theory
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 81 , Issue 3 , December 2006 , pp. 351 - 361
Copyright
Copyright © Australian Mathematical Society 2006

References

[1]David, F. N. and Barton, D. E., Combinatorial chance (Griffin, London, 1962).CrossRefGoogle Scholar
[2]Feller, W., An introduction to probability theory and its applications, Vol. 2 (Wiley, New York, 1966).Google Scholar
[3]Fisher, R. A., ‘Moments and product moments of sampling distributions’, Proc. London. Math. Soc. (2) 30 (1929), 200–238.Google Scholar
[4]Geary, R. C., ‘Distribution of “Student's” ratio for non-normal samples’, Suppl. J. Roy. Stat. Soc. 3 (1936), 178–184.CrossRefGoogle Scholar
[5]Kagan, A. M., Linnik, Yu. and Rao, C. R., Characterization problems in mathematical statistics (Wiley, New York, 1973).Google Scholar
[6]Kawata, T. and Sakamoto, H., ‘On the characterization of the normal population by the independence of the sample mean and the sample variance’, J. Math. Soc. Japan 1 (1949), 111–115.Google Scholar
[7]Kendall, M. G. and Stuart, A., The advanced theory of statistics, Vol. 1 Distribution Theory, 3rd edition (Griffin, London, 1969).Google Scholar
[8]Khinchin, A. Ya., ‘On unimodal distributions’, Izv. Nauk Mat. i Mekh. Inst. Tomsk 2 (1938), 1–7 (In Russian).Google Scholar
[9]Lukacs, E., ‘A characterization of the normal distribution’, Ann. Math. Stat. 13 (1956), 91–93.CrossRefGoogle Scholar
[10]Lukacs, E., ‘Characterization of populations by properties of suitable statistics’, Proc. Third Berkeley Symp. 2 (1956), 195–214.Google Scholar
[11]Quine, M. P., ‘On three characterizations of the normal distribution’, Probab. Math. Stat. 14 (1993), 257–263.Google Scholar
[12]Quine, M. P. and Seneta, E., ‘The generalization of the Kac-Bernstein theorem’, Probab. Math. Stat. 19 (1999), 441–452.Google Scholar
[13]Rao, C. R. and Shanbhag, D. N., Choquet-Deny type functional equations with applications to stochastic models (Wiley, New York, 1994).Google Scholar