Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
2005.
Topological Algebras with Involution.
Vol. 200,
Issue. ,
p.
451.
Toma, Aida
2009.
Integral representation for powers of elements in locally m-convex algebras and applications.
Rendiconti del Circolo Matematico di Palermo,
Vol. 58,
Issue. 1,
p.
29.

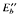 of a unital infrabarrelled l.m.c.
of a unital infrabarrelled l.m.c. 