Article contents
OBSTRUCTIONS TO A GENERAL CHARACTERIZATION OF GRAPH CORRESPONDENCES
Part of:
Selfadjoint operator algebras
Published online by Cambridge University Press: 07 June 2013
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
For a countable discrete space  $V$, every nondegenerate separable
$V$, every nondegenerate separable 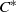 ${C}^{\ast } $-correspondence over
${C}^{\ast } $-correspondence over 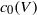 ${c}_{0} (V)$ is isomorphic to one coming from a directed graph with vertex set
${c}_{0} (V)$ is isomorphic to one coming from a directed graph with vertex set 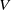 $V$. In this paper we demonstrate why the analogous characterizations fail to hold for higher-rank graphs (where one considers product systems of
$V$. In this paper we demonstrate why the analogous characterizations fail to hold for higher-rank graphs (where one considers product systems of 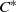 ${C}^{\ast } $-correspondences) and for topological graphs (where
${C}^{\ast } $-correspondences) and for topological graphs (where 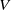 $V$ is locally compact Hausdorff), and we discuss the obstructions that arise.
$V$ is locally compact Hausdorff), and we discuss the obstructions that arise.
MSC classification
Secondary:
46L08: $C^*$-modules
- Type
- Research Article
- Information
- Copyright
- Copyright ©2013 Australian Mathematical Publishing Association Inc.
References
Abadie, B. and Exel, R., ‘Hilbert  ${C}^{\ast } $-bimodules over commutative
${C}^{\ast } $-bimodules over commutative  ${C}^{\ast } $-algebras and an isomorphism condition for quantum Heisenberg manifolds’, Rev. Math. Phys. 9 (4) (1997), 411–423.CrossRefGoogle Scholar
${C}^{\ast } $-algebras and an isomorphism condition for quantum Heisenberg manifolds’, Rev. Math. Phys. 9 (4) (1997), 411–423.CrossRefGoogle Scholar
Brown, L., Green, P. and Rieffel, M., ‘Stable isomorphism and strong Morita equivalence of  ${C}^{\ast } $-algebras’, Pacific J. Math. 71 (1977), 349–363.CrossRefGoogle Scholar
${C}^{\ast } $-algebras’, Pacific J. Math. 71 (1977), 349–363.CrossRefGoogle Scholar
Dixmier, J. and Douady, A., ‘Champs continus d’espaces hilbertiens et de  ${C}^{\ast } $-algèbres’, Bull. Soc. Math. France 91 (1963), 227–284.CrossRefGoogle Scholar
${C}^{\ast } $-algèbres’, Bull. Soc. Math. France 91 (1963), 227–284.CrossRefGoogle Scholar
Dupré, M. J. and Gillette, R. M., Banach Bundles, Banach Modules and Automorphisms of C*-algebras, Research Notes in Mathematics, 92 (Pitman, Boston).Google Scholar
Fowler, N. J. and Sims, A., ‘Product systems over right-angled Artin semigroups’, Trans. Amer. Math. Soc. 354 (2002), 1487–1509.CrossRefGoogle Scholar
Kaliszewski, S., Patani, N. and Quigg, J., ‘Characterizing graph  ${C}^{\ast } $-correspondences’, Houston J. Math. 38 (2012), 751–759.Google Scholar
${C}^{\ast } $-correspondences’, Houston J. Math. 38 (2012), 751–759.Google Scholar
Kumjian, A. and Pask, D., ‘Higher rank graph  ${C}^{\ast } $-algebras’, New York J. Math. 6 (2000), 1–20.Google Scholar
${C}^{\ast } $-algebras’, New York J. Math. 6 (2000), 1–20.Google Scholar
Kumjian, A., Pask, D. and Sims, A., ‘Homology for higher-rank graphs and twisted  ${C}^{\ast } $-algebras’, J. Funct. Anal. 263 (2012), 1539–1574.CrossRefGoogle Scholar
${C}^{\ast } $-algebras’, J. Funct. Anal. 263 (2012), 1539–1574.CrossRefGoogle Scholar
Patani, N., ‘ ${C}^{\ast } $-correspondences and topological dynamical systems associated to generalizations of directed graphs’, PhD Thesis, Arizona State University, 2011.Google Scholar
${C}^{\ast } $-correspondences and topological dynamical systems associated to generalizations of directed graphs’, PhD Thesis, Arizona State University, 2011.Google Scholar
Raeburn, I., ‘On the Picard group of a continuous trace  ${C}^{\ast } $-algebra’, Trans. Amer. Math. Soc. 263 (1981), 183–205.Google Scholar
${C}^{\ast } $-algebra’, Trans. Amer. Math. Soc. 263 (1981), 183–205.Google Scholar
Raeburn, I., Graph Algebras, CBMS Regional Conference Series in Mathematics, 103 (American Mathematical Society, Providence, RI, 2005).CrossRefGoogle Scholar
Raeburn, I. and Sims, A., ‘Product systems of graphs and the Toeplitz algebras of higher-rank graphs’, J. Operator Theory 53 (2005), 399–429.Google Scholar
Raeburn, I. and Williams, D. P., Morita Equivalence and Continuous-trace C ∗-algebras, Mathematical Surveys and Monographs, 60 (American Mathematical Society, Providence, RI, 1998).CrossRefGoogle Scholar
Takahashi, A., ‘A duality between Hilbert modules and fields of Hilbert spaces’, Rev. Colombiana Mat. 13 (2) (1979), 93–120.Google Scholar
Takahashi, A., ‘Hilbert modules and their representation’, Rev. Colombiana Mat. 13 (1) (1979), 1–38.Google Scholar
Vasselli, E., ‘Continuous fields of  ${C}^{\ast } $-algebras arising from extensions of tensor
${C}^{\ast } $-algebras arising from extensions of tensor  ${C}^{\ast } $-categories’, J. Funct. Anal. 199 (1) (2003), 122–152.CrossRefGoogle Scholar
${C}^{\ast } $-categories’, J. Funct. Anal. 199 (1) (2003), 122–152.CrossRefGoogle Scholar
- 1
- Cited by


