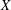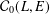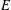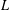Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Dantas, Sheldon
García, Domingo
Maestre, Manuel
and
Roldán, Óscar
2022.
Operator and Norm Inequalities and Related Topics.
p.
519.
Grando, T.
and
Lourenço, M. L.
2025.
The Bishop-Phelps-Bollobás property for operators defined on $$c_0$$-sum of Euclidean spaces.
Analysis Mathematica,
Vol. 51,
Issue. 1,
p.
211.