Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-28T20:36:35.585Z Has data issue: false hasContentIssue false
  • English
  • Français

On continuation of quasi-analytic solutions of partial differential equations to compact convex sets

Part of: Partial differential equations Equations and systems with constant coefficients

Published online by Cambridge University Press:  09 April 2009

Wojciech Abramczuk
Wojciech Abramczuk
Affiliation:
Department of Mathematics, University of Stockholm, Stockholm, Sweden
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In the early 70s A. Kaneko studied the problem of continuation of regular solutions of systems of linear partial differential equations with constant coefficients to compact convex sets. We show here that the conditions be obtained for real analytic solutions also hold in the quasi-analytic case. In particular we show that every quasi-analytic solution of the system p(D)u = 0 defined outside a compact convex subset K or Rn can be continued as a quasi-analytic solution to K if and only if the system is determined and the 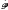-module Ext1(Coker p′, 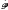) has no elliptic component; here 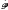is the ring of polynomials in n variables, p is a matrix with elements from 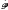and p′ is the transposed matrix. In the scalar case, i.e. when p is a single polynomial, these conditions mean that p has no elliptic factor.

Keywords

partial differential equationscontinuation of solutionsremovable singularitiesquasi-analytic functions

MSC classification

Secondary: 35B60: Continuation and prolongation of solutions 35E99: None of the above, but in this section
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 39 , Issue 3 , December 1985 , pp. 306 - 316
Copyright
Copyright © Australian Mathematical Society 1985

References

[1]Björk, J. E., Rings of differential operators (North-Holland, Amsterdam, 1979).Google Scholar
[2]Boas, R. P., Entire functions (Academic Press, New York, 1954).Google Scholar
[3]Bochner, S., ‘Partial differential equations and analytic continuation’, Proc. Nat. Acad. Sci. 38 (1952), 227–230.CrossRefGoogle Scholar
[4]Boman, J., ‘On the propagation of analyticity of solutions of differential equations with constant coefficients’, Ark. Mat. 5 (1964), 271–279.CrossRefGoogle Scholar
[5]Ehrenpreis, L., ‘A new proof and an extension of Hartogs' theorem’, Bull. Amer. Math. Soc. 67 (1961), 507–509.CrossRefGoogle Scholar
[6]Grušin, V. V., ‘On solutions with isolated singularities for partial differential equations with constant coefficients’, Trudy Moskov. Mat. Obšč. 15 (1966), 262–278 (in russian).Google Scholar
[7]Hartogs, F., ‘Einige Folgerungen aus der Cauchyschen Integralformel bei Funktionen mehrer Veränderlichen’, Sitzb. Münchener Acad. 36 (1906), 223.Google Scholar
[8]Hörmander, L., ‘Between distributions and hyperfunctions’, (Proc. Colloq. L. Schwartz, 1983, to appear in Astérisque).Google Scholar
[9]Kaneko, A., ‘On continuation of regular solutions of partial differential equations to compact convex sets’, J. Fac. Univ. Tokyo, Sect IA, 17 (1970), 567–580.Google Scholar
[10]Kaneko, A., ‘On continuation of regular solutions of partial differential equations to compact convex sets’, J. Fac. Univ. Tokyo, Sect IA 18 (1972), 415–433.Google Scholar
[11]Kaneko, A., ‘Note on continuation of real analytic solutions of partial differential equations with constant coefficients’, Proc. Japan Acad. 51 (1975), 262–264.CrossRefGoogle Scholar
[12]Kaneko, A., ‘Prolongement des solutions analytiques réelles d'équations aux dérivées partielles á coefficients constants’ (Sém. Goulaouic-Schwartz 1976–1977, Exposé n° XVIII).Google Scholar
[13]Kaneko, A., ‘On continuation of real analytic solutions of linear partial differential equations’, Astérisque 89– 90 (1981), 11–44.Google Scholar
[14]Komatsu, H., ‘Relative cohomology of sheaves of solutions of differential equations’ (Séminaire Lions-Schwartz 1966–67. Reprinted in Lecture Notes in Math. 287, Springer, 1973, pp. 192–261).Google Scholar
[15]Lech, C., ‘A metric property of the zeros of a complex polynomial ideal’, Ark. Mat. 3 (1958), 543–554.CrossRefGoogle Scholar
[16]Malgrange, B., ‘Sur les systélmes différentiels ά coefficients constants’ (Séminaire Leray, 1961–1962).Google Scholar
[17]Matsuura, S., ‘On general systems of partial differential equations with constant coefficients’, J. Math. Soc. Japan. 13 (1961), 94–103.CrossRefGoogle Scholar
[18]Palamodov, V. P., Linear differential operators with constant coefficients (Grundlehren 168, Springer-Verlag, Berlin, 1970).CrossRefGoogle Scholar
[19]Riemann, B., ‘Grundlagen für eine allgemeine Theorie der Funktionen einer veränderlichen complexen Grösse’, pp. 3–48, Gesam. Math. Werke.Google Scholar