Article contents
On distributions whose moments are majorated by the moments of a known distribution*
Published online by Cambridge University Press: 09 April 2009
Summary
Let F(x) be a distribution function and denote by 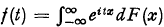 its characteristic function and by
its characteristic function and by 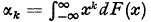 its moment of order k H. Milicer-Grużewska [2]has derived the following theorem: Suppose that F(x) has moments of all orders and that they satisfy the relations.
its moment of order k H. Milicer-Grużewska [2]has derived the following theorem: Suppose that F(x) has moments of all orders and that they satisfy the relations.  where
where  while C is a positive constant. Then f(t) is an entire function of order not exceeding two. The proof given by H. Milicer-Gruzewska is rather complicated, moreover the restriction (1.2) seems to be artificial and motivated only by the particular method of proof. We note that condition (1.1) means that the moments of F (x) are majorated by the moments of a normal distribution and we use this remark to generalize the problem.
while C is a positive constant. Then f(t) is an entire function of order not exceeding two. The proof given by H. Milicer-Gruzewska is rather complicated, moreover the restriction (1.2) seems to be artificial and motivated only by the particular method of proof. We note that condition (1.1) means that the moments of F (x) are majorated by the moments of a normal distribution and we use this remark to generalize the problem.
- Type
- Research Article
- Information
- Copyright
- Copyright © Australian Mathematical Society 1959
References
- 1
- Cited by


