Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Janakiraman, S.
and
Rangaswamy, K. M.
1977.
Group Theory.
Vol. 573,
Issue. ,
p.
57.
Hiremath, V. A.
1978.
Finitely projective modules over a Dedekind domain.
Journal of the Australian Mathematical Society,
Vol. 26,
Issue. 3,
p.
330.
Faith, Carl
1979.
Self-injective rings.
Proceedings of the American Mathematical Society,
Vol. 77,
Issue. 2,
p.
157.
Takeuchi, Tsutomu
1984.
A note on $M$-projective modules, II.
Proceedings of the Japan Academy, Series A, Mathematical Sciences,
Vol. 60,
Issue. 5,
Azumaya, Goro
1987.
Finite splitness and finite projectivity.
Journal of Algebra,
Vol. 106,
Issue. 1,
p.
114.
Azumaya, Goro
1990.
Non-Commutative Ring Theory.
Vol. 1448,
Issue. ,
p.
1.
Naoum, Adil G.
1995.
Regular multiplication modules.
Periodica Mathematica Hungarica,
Vol. 31,
Issue. 2,
p.
155.
Gray, D. J.
1997.
ON RELATIVE INJECTIVITY.
Quaestiones Mathematicae,
Vol. 20,
Issue. 4,
p.
569.
Xue, Weimin
1998.
Artinian rings with Morita duality.
Science in China Series A: Mathematics,
Vol. 41,
Issue. 12,
p.
1233.
Zimmermann, Wolfgang
2002.
On locally pure-injective modules.
Journal of Pure and Applied Algebra,
Vol. 166,
Issue. 3,
p.
337.
Couchot, F.
2003.
Injective modules and fp-injective modules over valuation rings.
Journal of Algebra,
Vol. 267,
Issue. 1,
p.
359.
Couchot, F.
2007.
Flat modules over valuation rings.
Journal of Pure and Applied Algebra,
Vol. 211,
Issue. 1,
p.
235.
Zhang, Xiaoxiang
and
Chen, Jianlong
2008.
Properties of Modules and Rings Relative to Some Matrices.
Communications in Algebra,
Vol. 36,
Issue. 10,
p.
3682.
Couchot, François
2009.
Localization of Injective Modules Over Arithmetical Rings.
Communications in Algebra,
Vol. 37,
Issue. 10,
p.
3418.
Smith, Patrick F.
2012.
On injective and divisible modules.
Arabian Journal of Mathematics,
Vol. 1,
Issue. 1,
p.
127.
Abduldaim, Areej M.
and
Chen, Sheng
2013.
-Regular Modules.
Journal of Applied Mathematics,
Vol. 2013,
Issue. ,
p.
1.
Zhang, Jun
Wang, Fanggui
and
Kim, Hwankoo
2013.
INJECTIVE MODULES OVER ω-NOETHERIAN RINGS, II.
Journal of the Korean Mathematical Society,
Vol. 50,
Issue. 5,
p.
1051.
Banerjee, Abhishek
2016.
Some remarks on a theorem of Bergman.
Comptes Rendus. Mathématique,
Vol. 354,
Issue. 7,
p.
665.
Hassanzadeh-Lelekaami, Dawood
and
Roshan-Shekalgourabi, Hajar
2019.
On Regular Modules over Commutative Rings.
Bulletin of the Malaysian Mathematical Sciences Society,
Vol. 42,
Issue. 2,
p.
569.
Anderson, D. D.
Chun, Sangmin
and
Juett, J. R.
2019.
Module-theoretic generalization of commutative von Neumann regular rings.
Communications in Algebra,
Vol. 47,
Issue. 11,
p.
4713.
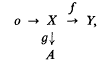 where X is finitely generated and the row is exact, can be imbedded in a commutative diagram
where X is finitely generated and the row is exact, can be imbedded in a commutative diagram 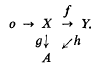 The finitely injective modules turn out to have the nice property of being ‘strongly pure’ in all the containing modules and, in particular, are absolutely pure in the sense of Maddox [8]. For this reason we call them strongly absolutely pure (for short, SAP) modules. Several other characterizations of the SAP modules are obtained. It is shown that every module admits a ‘SAP hull’. The concepts of finitely M-injective and finitely quasi-injective modules are then investigated. A subclass of finitely quasi-injective modules, called the strongly regular modules, is studied in some detail and it is shown that, if R/J is right Noetherian, then the strongly regular right R-modules coincide with the semi-simple R-modules.
The finitely injective modules turn out to have the nice property of being ‘strongly pure’ in all the containing modules and, in particular, are absolutely pure in the sense of Maddox [8]. For this reason we call them strongly absolutely pure (for short, SAP) modules. Several other characterizations of the SAP modules are obtained. It is shown that every module admits a ‘SAP hull’. The concepts of finitely M-injective and finitely quasi-injective modules are then investigated. A subclass of finitely quasi-injective modules, called the strongly regular modules, is studied in some detail and it is shown that, if R/J is right Noetherian, then the strongly regular right R-modules coincide with the semi-simple R-modules.

