Hostname: page-component-78c5997874-lj6df Total loading time: 0 Render date: 2024-11-10T16:10:02.481Z Has data issue: false hasContentIssue false
  • English
  • Français

ON GENERALISED FC-GROUPS IN WHICH NORMALITY IS A TRANSITIVE RELATION

Part of: Special aspects of infinite or finite groups Structure and classification of infinite or finite groups

Published online by Cambridge University Press:  29 October 2015

R. ESTEBAN-ROMERO  and
G. VINCENZI
R. ESTEBAN-ROMERO
Affiliation:
Institut Universitari de Matemàtica Pura i Aplicada, Universitat Politècnica de València, Camí de Vera, s/n, 46022 València, Spain email resteban@mat.upv.es
G. VINCENZI*
Affiliation:
Dipartimento di Matematica e Informatica, Università di Salerno, Via Giovanni Paolo II, Fisciano, 132, 84084 Salerno, Italy email gvincenzi@unisa.it
*
✉gvincenzi@unisa.it
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We extend to soluble 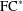$\text{FC}^{\ast }$-groups, the class of generalised FC-groups introduced in de Giovanni et al. [‘Groups with restricted conjugacy classes’, Serdica Math. J. 28(3) (2002), 241–254], the characterisation of finite soluble T-groups obtained recently in Kaplan [‘On T-groups, supersolvable groups, and maximal subgroups’, Arch. Math. (Basel) 96(1) (2011), 19–25].

Keywords

T-groupFC-grouppronormal subgroup

MSC classification

Primary: 20F24: FC-groups and their generalizations
Secondary: 20E34: General structure theorems 20F14: Derived series, central series, and generalizations 20F19: Generalizations of solvable and nilpotent groups
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 100 , Issue 2 , April 2016 , pp. 192 - 198
Copyright
© 2015 Australian Mathematical Publishing Association Inc. 

References

Ballester-Bolinches, A. and Esteban-Romero, R., ‘On finite 𝓣-groups’, J. Aust. Math. Soc. Ser. A 75 (2003), 1–11.Google Scholar
Ballester-Bolinches, A., Esteban-Romero, R. and Asaad, M., Products of Finite Groups, de Gruyter Expositions in Mathematics, 53 (Walter de Gruyter, Berlin, 2010).CrossRefGoogle Scholar
Bianchi, M., Gillio Berta Mauri, A., Herzog, M. and Verardi, L., ‘On finite solvable groups in which normality is a transitive relation’, J. Group Theory 3(2) (2000), 147–156.Google Scholar
de Giovanni, F., Russo, A. and Vincenzi, G., ‘Groups with restricted conjugacy classes’, Serdica Math. J. 28(3) (2002), 241–254.Google Scholar
de Giovanni, F. and Vincenzi, G., ‘Pronormality in infinite groups’, Math. Proc. R. Ir. Acad. 100A(2) (2000), 189–203.Google Scholar
de Giovanni, F. and Vincenzi, G., ‘Some topics in the theory of pronormal subgroups of groups’, in: Topics in Infinite Groups, Quaderni di Matematica, 8 (Aracne Ed and Dipartimento di Matematica, Seconda Università di Napoli, Caserta, 2001), 175–202.Google Scholar
Gaschütz, W., ‘Gruppen, in denen das Normalteilersein transitiv ist’, J. reine angew. Math. 198 (1957), 87–92.Google Scholar
Imperatore, D., Russo, A. and Vincenzi, G., ‘Groups whose proper subgroups are generalized FC-groups’, J. Algebra Appl. 10(6) (2011), 1301–1308.CrossRefGoogle Scholar
Kaplan, G., ‘On finite T-groups and the Wielandt subgroup’, J. Group Theory 14 (2011), 855–863.CrossRefGoogle Scholar
Kaplan, G., ‘On T-groups, supersolvable groups, and maximal subgroups’, Arch. Math. (Basel) 96(1) (2011), 19–25.Google Scholar
Kaplan, G. and Vincenzi, G., ‘On the Wielandt subgroup of generalized FC-groups’, Int. J. Algebra Comput. 24(7) (2014), 1031–1042.Google Scholar
Kovács, L. G., Neumann, B. H. and de Vries, H., ‘Some sylow subgroups’, Proc. R. Soc. Ser. A 260 (1961), 304–316.Google Scholar
Kuzennyi, N. F. and Subbotin, I. Ya., ‘Groups in which all subgroups are pronormal’, Ukrainian Math. J. 39(3) (1987), 251–254.CrossRefGoogle Scholar
Peng, T. A., ‘Finite groups with pronormal subgroups’, Proc. Amer. Math. Soc. 20 (1969), 232–234.Google Scholar
Robinson, D. J. S., ‘Groups in which normality is a transitive relation’, Math. Proc. Cambridge Philos. Soc. 60 (1964), 21–38.Google Scholar
Robinson, D. J. S., Finiteness Conditions and Generalized Soluble Groups (Springer, Berlin, 1972).Google Scholar
Robinson, D. J. S., Russo, A. and Vincenzi, G., ‘On groups which contain no HNN-extensions’, Int. J. Algebra Comput. 17(7) (2007), 1377–1387.CrossRefGoogle Scholar
Robinson, D. J. S., Russo, A. and Vincenzi, G., ‘On the theory of generalized FC-groups’, J. Algebra 326 (2011), 218–226.Google Scholar
Romano, E. and Vincenzi, G., ‘Pronormality in generalized FC-groups’, Bull. Aust. Math. Soc. 83 (2011), 220–230.Google Scholar
Romano, E. and Vincenzi, G., ‘Groups in which normality is a weakly transitive relation’, J. Algebra Appl. 14(1) (2015), 1550007 (12 pages).Google Scholar
Tortora, A. and Vincenzi, G., ‘The Engel elements in generalized FC-groups’, Illinois J. Math. 58(2) (2014), 577–583.Google Scholar
Zacher, G., ‘Caratterizzazione dei t-gruppi finiti risolubili’, Ric. Mat. 1 (1952), 287–294.Google Scholar