Hostname: page-component-78c5997874-lj6df Total loading time: 0 Render date: 2024-11-10T17:38:29.007Z Has data issue: false hasContentIssue false
  • English
  • Français

On graph C*-algebras

Part of: Selfadjoint operator algebras

Published online by Cambridge University Press:  09 April 2009

P. Goldstein
P. Goldstein
Affiliation:
School of Mathematics, Cardiff UniversityP.O.Box 926, cardiff CF24 4YH e-mail: goldsteinp@cardiff.ac.uk
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Certain C*-algebras on generators and relations are associated to directed graphs. For a finite graph γ, C*-algebra 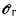is canonically isomorphic to Cuntz-Krieger algebra corresponding to the adjacency matrix of γ. It is shown that if a countably infinite graph γ is strongly connected, 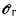γ is simple and purely infinite.

MSC classification

Secondary: 46L05: General theory of $C^*$-algebras 46L35: Classifications of $C^*$-algebras
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 72 , Issue 2 , April 2002 , pp. 153 - 160
Copyright
Copyright © Australian Mathematical Society 2002

References

[1]Cuntz, J., ‘Simple C*-algebras generated by isometries’, Comm. Math. Phys. 57 (1977), 173–185.Google Scholar
[2]Cuntz, J., ‘A class of C*-algebras and topological markov chains II’, Invent.Math. 63 (1981), 25–40.CrossRefGoogle Scholar
[3]Cuntz, J., ‘K-theory for certain C*-algebras’, Ann. of Math. (2) 113 (1981), 181–197.CrossRefGoogle Scholar
[4]Cuntz, J. and Krieger, W., ‘A class of C*-algebras and topological Markov chains’, Invent. Math. 56 (1980), 251–268.CrossRefGoogle Scholar
[5]Evans, D. E., ‘Gauge actions on ’, J. Operator Theory 7 (1982), 79–100.Google Scholar
[6]Exel, R. and Laca, M., ‘Cuntz-Krieger algebras for infinite matrices’, J. Reine Angew. Math. 512 (1999), 119–172.CrossRefGoogle Scholar
[7]Exel, R. and Laca, M., ‘The K-theory of Cuntz-Krieger algebras for infinite matrices’, K-theory 19 (2000), 251–268.Google Scholar
[8]Goldstein, P., ‘Classification of canonical Z2-actions on ∞’, preprint.Google Scholar
[9]Hancock, R. and Raeburn, I., ‘The C*-algebras of some inverse semigroups’, Bull. Aystral. Math. Soc. 42 (1990), 335–348.Google Scholar
[10]Izumi, M., ‘Subalgebras of infinite C*-algebras with finite Watatani indices II. Cuntz-krieger algebras’, Duke Math. J. 91 (1998), 409–461.Google Scholar
[11]Katayama, Y., Matsumoto, K. and Watatani, Y., ‘Simple C*-algebras arising from β-expansion of real numbers’, Ergodic Theory Dynam. Systems 18 (1998), 937–962.Google Scholar
[12]Kirchberg, E., ‘The classification of purely infinite C*-algebras using Kasparov's theory’, preprint, (Fiedls Institute, 1994).Google Scholar
[13]Krichberg, E. and Phillips, N. C., ‘Embedding of exact C*-algebras in the Cuntz algebra2’, J. Reine Angew. Math. 525 (2000), 17–53.Google Scholar
[14]Kumjian, A., Pask, D. and Raeburn, I., ‘Cuntz-Krieger algebras of directed graphs’, Pacific J. Math. 184 (1998), 161–174.Google Scholar
[15]Pask, D and Raeburn, I., ‘On the K-theory of Cuntz-krieger algebras’, Publ. Res. Inst. Math. Sci. 32 (1996), 415–443.Google Scholar
[16]Pimsner, M., ‘A class of C*-algebras generalizing both Cuntz-Krieger algebras and crossed products by Z’, in: Free probability theory (Waterloo, ON, 1995), Fields Inst. Commun. 12 (Amer. Math. Soc., Providence, RI, 1997) pp. 189–212.Google Scholar