Article contents
ON HIGHER DIMENSIONAL ARITHMETIC PROGRESSIONS IN MEYER SETS
Published online by Cambridge University Press: 06 December 2021
Abstract
In this paper we study the existence of higher dimensional arithmetic progressions in Meyer sets. We show that the case when the ratios are linearly dependent over  ${\mathbb Z}$ is trivial and focus on arithmetic progressions for which the ratios are linearly independent. Given a Meyer set
${\mathbb Z}$ is trivial and focus on arithmetic progressions for which the ratios are linearly independent. Given a Meyer set 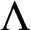 $\Lambda $ and a fully Euclidean model set
$\Lambda $ and a fully Euclidean model set 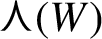 with the property that finitely many translates of
with the property that finitely many translates of  cover
cover 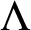 $\Lambda $, we prove that we can find higher dimensional arithmetic progressions of arbitrary length with k linearly independent ratios in
$\Lambda $, we prove that we can find higher dimensional arithmetic progressions of arbitrary length with k linearly independent ratios in 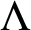 $\Lambda $ if and only if k is at most the rank of the
$\Lambda $ if and only if k is at most the rank of the  ${\mathbb Z}$-module generated by
${\mathbb Z}$-module generated by 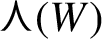 . We use this result to characterize the Meyer sets that are subsets of fully Euclidean model sets.
. We use this result to characterize the Meyer sets that are subsets of fully Euclidean model sets.
MSC classification
Information
- Type
- Research Article
- Information
- Copyright
- © The Author(s), 2021. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.
Footnotes
Communicated by Michael Coons
The work was supported by NSERC with grant 2020-00038; we are grateful for the support.
References
- 2
- Cited by


