Hostname: page-component-78c5997874-s2hrs Total loading time: 0 Render date: 2024-11-14T23:47:50.545Z Has data issue: false hasContentIssue false
  • English
  • Français

On product varieties of inverse semigroups

Published online by Cambridge University Press:  09 April 2009

J. L. Bales
J. L. Bales
Affiliation:
Department of Mathematics Monash UniversityClayton, Victoria 3168, Australia
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

This paper extends results on product varieties of groups to inverse semigroups. We show that if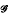 is a variety of groups and 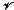any inverse semigroup variety, then 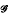∘ 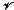is a variety. We give a characterization of the identities of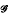∘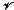in terms of the identities of 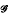and of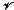We show that if 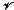does not contain the variety of all groups then it has uncountably many supervarieties. Finally we show that if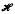is another variety of groups then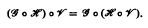

Subject classifiaction (Amer. Math. Soc. (MOS) 1970): 20 M 05.

Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 28 , Issue 1 , August 1979 , pp. 107 - 119
Copyright
Copyright © Australian Mathematical Society 1979

References

Clifford, A. H. and Preston, G. B. (1961, 1967), The algebraic theory of semigroups, Vols. 1 and 2 (Amer. Math. Soc, Math. Surveys 7, Providence).Google Scholar
Grätzer, G. (1968), Universal algebra (Van Nostrand).Google Scholar
Houghton, C. H. (1976), ‘Embedding inverse semigroups in wreath products’, Glasgow Math. J. 17, 77–82.CrossRefGoogle Scholar
Howie, J. M. (1964), ‘The maximum idempotent separating congruence on an inverse semigroup’, Proc. Edinburgh Math. Soc. (2) 14, 71–79.CrossRefGoogle Scholar
Maltsev, A. I. (1967), ‘Multiplication of classes of algebraic systems’, Sib. Mat. Z. 8, 346–365 (Russian).Google Scholar
Munn, W. D. (1974), ‘Free inverse semigroups’, Proc. London Math. Soc. (3) 29, 385–404.CrossRefGoogle Scholar
Neumann, H. (1967), Varieties of groups (Ergebnisse d. Math. u. i. Grenzgebiete, Bd. 37, Springer-Verlag, Berlin).CrossRefGoogle Scholar
Petrich, M. (1975), ‘Varieties of orthodox bands of groups’, Pacific J. of Math. 58, 209–217.CrossRefGoogle Scholar
Scheiblich, H. E. (1973), ‘Free inverse semigroups’, Proc. Amer. Math. Soc. 38, 1–7.CrossRefGoogle Scholar
Vaughn-Lee, M. R. (1970), ‘Uncountably many varieties of groups’, Bull. London Math. Soc. 2, 280–286.CrossRefGoogle Scholar