Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
1975.
On Measures of Information and their Characterizations.
Vol. 115,
Issue. ,
p.
219.
Aczél, J.
1975.
A Modern Course on Statistical Distributions in Scientific Work.
p.
321.
Walter, Wolfgang
1976.
Remark on a paper by Aczél and Ostrowski.
Journal of the Australian Mathematical Society,
Vol. 22,
Issue. 2,
p.
165.
Katok, A. B.
Sinai, Ya. G.
and
Stepin, A. M.
1977.
Theory of dynamical systems and general transformation groups with invariant measure.
Journal of Soviet Mathematics,
Vol. 7,
Issue. 6,
p.
974.
Fischer, Thomas R. M.
1978.
Transactions of the Eighth Prague Conference.
p.
211.
Aczel, J.
1978.
Some Recent Results on characterizations of Measures of Information Related to Coding.
IEEE Transactions on Information Theory,
Vol. 24,
Issue. 5,
p.
592.
Aczél, J.
Fischer, P.
and
Kardos, P.
1980.
General Inequalities 2.
Vol. 47,
Issue. ,
p.
441.
Aczél, J
1980.
A mixed theory of information. V. How to keep the (inset) expert honest.
Journal of Mathematical Analysis and Applications,
Vol. 75,
Issue. 2,
p.
447.
CAPOCELLI, RENATO M.
and
TANEJA, INDER JEET
1985.
ON SOME INEQUALITIES AND GENERALIZED ENTROPIES: A UNIFIED APPROAC.
Cybernetics and Systems,
Vol. 16,
Issue. 4,
p.
341.
Aczél, J.
1987.
Uncertainty in Knowledge-Based Systems.
Vol. 286,
Issue. ,
p.
357.
Kannappan, P.L.
and
Sahoo, P.K.
1989.
On a generalization of the Shannon functional inequality.
Journal of Mathematical Analysis and Applications,
Vol. 140,
Issue. 2,
p.
341.
Mitrinović, D. S.
Pečarić, J. E.
and
Fink, A. M.
1993.
Classical and New Inequalities in Analysis.
p.
635.
Hazewinkel, M.
1997.
Encyclopaedia of Mathematics.
p.
325.
Sahoo, Prasanna K.
2000.
Survey on Classical Inequalities.
p.
203.
Ng, Che Tat
2010.
Tribute to a Distinguished Professor János Aczél at 85.
Aequationes mathematicae,
Vol. 80,
Issue. 1-2,
p.
1.
Olbryś, Andrzej
2019.
On a problem of T. Szostok concerning the Hermite–Hadamard inequalities.
Journal of Mathematical Analysis and Applications,
Vol. 475,
Issue. 1,
p.
41.


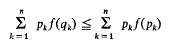
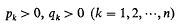
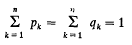 were given and the following was proved.
were given and the following was proved.