Hostname: page-component-78c5997874-fbnjt Total loading time: 0 Render date: 2024-11-13T08:36:00.363Z Has data issue: false hasContentIssue false
  • English
  • Français

On the construction of convergent iterative sequences of polynomials

Part of: Entire and meromorphic functions, and related topics

Published online by Cambridge University Press:  09 April 2009

Qiu Weiyuan
Qiu Weiyuan
Affiliation:
Institute of Mathematics Fudan UniversityShangai People's Republic of, China
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We answer two conjectures suggested by Zalman Rubinstein. We prove his Conjecture 1, that is, we construct convergent iterative sequences for 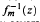with an arbitrary initial point, where 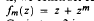with m ≥ 2. We also show by several counterexamples that Rubinstein's Conjecture 2 is generally false.

MSC classification

Secondary: 30D05: Functional equations in the complex domain, iteration and composition of analytic functions
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 47 , Issue 3 , December 1989 , pp. 382 - 390
Copyright
Copyright © Australian Mathematical Society 1989

References

[1]Rubinstein, Zalman, ‘A variational method for the construction of convergent iterative sequences’, J. Austral. Math. Soc. Ser. A 41 (1986), 51–58.CrossRefGoogle Scholar
[2]Brolin, H., ‘Invariant sets under iteration of rational functions’, Ark. Mat. 6 (1965), 103–144.CrossRefGoogle Scholar
[3]Fatou, P., ‘Sur les équations fonctionelles’, Bull. Soc. Math. France 47 (1919), 161–271.CrossRefGoogle Scholar
[4]Fatou, P., ‘Sur l'itération des fonctions transcendantes entieres’, Acta Math. 47 (1926), 337–370.CrossRefGoogle Scholar
[5]Julia, G., ‘Memoire sur l'itération des fonctions rationnelles’, J. Math. Pures Appl. (8) 1 (1918), 47–245.Google Scholar
[6]Baker, I. N., ‘Permutable power series and regular iteration’, J. Austral. Math. Soc. 2 (1962), 265–194.CrossRefGoogle Scholar
[7]Seigel, C., ‘Iteration of analtyic functions’, Ann. of Math. (2) 43 (1942), 607–612.CrossRefGoogle Scholar