Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-26T17:58:48.892Z Has data issue: false hasContentIssue false
  • English
  • Français

On the faithful representations, of degree 2n, of certain extensions of 2-groups by orthogonal and symplectic groups

Part of: Linear algebraic groups and related topics Representation theory of groups

Published online by Cambridge University Press:  09 April 2009

S. P. Glasby
S. P. Glasby
Affiliation:
School of Mathematics and Statistics, The University of Sydney, NSW 2006, Australia
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

If R is a 2-group of symplectic type with exponent 4, then R is isomorphic to the extraspecial group 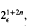, or to the central product 4 o 21+2n of a cyclic group of order 4 and an extraspecial group, with central subgroups of order 2 amalgamated. This paper gives an explicit description of a projective representation of the group A of automorphisms of R centralizing Z(R), obtained from a faithful representation of R of degree 2n. The 2-cocycle associated with this projective representation takes values which are powers of −1 if R is isomorphic to 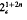and powers of 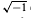otherwise. This explicit description of a projective representation is useful for computing character values or computing with central extensions of A. Such central extensions arise naturally in Aschbacher's classification of the subgroups of classical groups.

MSC classification

Secondary: 20C15: Ordinary representations and characters 20G05: Representation theory
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 58 , Issue 2 , April 1995 , pp. 232 - 247
Copyright
Copyright © Australian Mathematical Society 1995

References

[1]Aschbacher, M., ‘On the maximal subgroups of the finite classical groups’, Invent. Math. 76 (1984), 469–514.CrossRefGoogle Scholar
[2]Dieudonné, J., Sur les groupes classique (Hermann, Paris, 1984).Google Scholar
[3]Gérardin, P., ‘Weil representations associated to finite fields’, J. Algebra 46 (1977), 54–101.CrossRefGoogle Scholar
[4]Glasby, S. P. and Howlett, R. B., ‘Extraspecial towers and Weil representations’, J. Algebra 151 (1992), 236–260.CrossRefGoogle Scholar
[5]Gorenstein, D., Finite groups (Chelsea, New York, 1980).Google Scholar
[6]Greiss, R. L., ‘Automorphisms of extra special groups and nonvanishing degree 2 cohomology’, Pacific J. Math. 48 (1973), 402–422.Google Scholar
[7]Huppert, B., Endliche Gruppen I (Springer, Berlin, 1967).CrossRefGoogle Scholar
[8]Kleidman, P. and Liebeck, M., The subgroup structure of the finite classical groups, London Mathematical Society Lecture Note Series 129 (Cambridge Univ. Press, Cambridge, 1990).CrossRefGoogle Scholar
[9]Schur, I., ‘Über die Darstellung der endlichen Gruppen durch gebrochene linear Substitutionen’, J. Reine Angew. Math. 132 (1907), 85–137.Google Scholar
[10]Suzuki, M., Group Theory II (Springer, New York, 1986).CrossRefGoogle Scholar
[11]Taylor, D. E., The geometry of the classical groups, (Helderman, Berlin, 1992).Google Scholar
[12]Ward, H. N., ‘Representations of symplectic groups’, J. Algebra 20 (1974), 182–195.CrossRefGoogle Scholar