Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-10T13:57:23.441Z Has data issue: false hasContentIssue false
  • English
  • Français

ON THE GENERATING GRAPH OF A SIMPLE GROUP

Part of: Probabilistic methods in group theory Representation theory of groups

Published online by Cambridge University Press:  26 September 2016

ANDREA LUCCHINI ,
ATTILA MARÓTI  and
COLVA M. RONEY-DOUGAL
ANDREA LUCCHINI
Affiliation:
Dipartimento di Matematica, Università degli studi di Padova, Via Trieste 63, 35121 Padova, Italy email lucchini@math.unipd.it
ATTILA MARÓTI
Affiliation:
MTA Alfréd Rényi Institute of Mathematics, Reáltanoda utca 13–15, H-1053, Budapest, Hungary email maroti.attila@renyi.mta.hu
COLVA M. RONEY-DOUGAL*
Affiliation:
Mathematical Institute, University of St Andrews, St Andrews, Fife KY16 9SS, UK email colva.roney-dougal@st-andrews.ac.uk
*
✉colva.roney-dougal@st-andrews.ac.uk
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The generating graph 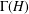$\unicode[STIX]{x1D6E4}(H)$ of a finite group 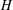$H$ is the graph defined on the elements of 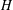$H$, with an edge between two vertices if and only if they generate 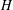$H$. We show that if 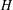$H$ is a sufficiently large simple group with 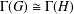$\unicode[STIX]{x1D6E4}(G)\cong \unicode[STIX]{x1D6E4}(H)$ for a finite group 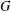$G$, then 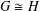$G\cong H$. We also prove that the generating graph of a symmetric group determines the group.

Keywords

generating graphfinite group

MSC classification

Primary: 20D06: Simple groups
Secondary: 20P05: Probabilistic methods in group theory
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 103 , Issue 1 , August 2017 , pp. 91 - 103
Copyright
© 2016 Australian Mathematical Publishing Association Inc. 

Footnotes

The authors were supported by Università di Padova (Progetto di Ricerca di Ateneo: Invariable generation of groups). The second author was also supported by an Alexander von Humboldt Fellowship for Experienced Researchers, by OTKA grants K84233 and K115799, and by the MTA Rényi Lendület Groups and Graphs Research Group.

References

Aschbacher, M., Finite Group Theory, Cambridge Studies in Advanced Mathematics, 10 (Cambridge University Press, Cambridge, 1986).Google Scholar
Bray, J. N., Holt, D. F. and Roney-Dougal, C. M., The Maximal Subgroups of the Low-Dimensional Finite Classical Groups, London Mathematical Society Lecture Note Series, 407 (Cambridge University Press, Cambridge, 2013).CrossRefGoogle Scholar
Breuer, T., Guralnick, R. M. and Kantor, W. M., ‘Probabilistic generation of finite simple groups. II’, J. Algebra 320(2) (2008), 443–494.CrossRefGoogle Scholar
Burness, T. C. and Guest, S., ‘On the uniform spread of almost simple linear groups’, Nagoya Math. J. 209 (2013), 35–109.CrossRefGoogle Scholar
Conway, J. H., Curtis, R. T., Norton, S. P., Parker, R. A. and Wilson, R. A., An ATLAS of Finite Groups (Clarendon Press, Oxford, 1985), reprinted with corrections 2003.Google Scholar
The GAP Group, GAP – ‘Groups, Algorithms, and Programming’, Version 4.7.7, 2015. http://www.gap-system.org.Google Scholar
Guralnick, R. M., ‘The spread of finite groups’, in preparation.Google Scholar
Guralnick, R. M. and Kantor, W. M., ‘Probabilistic generation of finite simple groups. Special issue in honor of Helmut Wielandt’, J. Algebra 234(2) (2000), 743–792.CrossRefGoogle Scholar
Häsä, J., ‘Growth of cross-characteristic representations of finite quasisimple groups of Lie type’, J. Algebra 407 (2014), 275–306.CrossRefGoogle Scholar
Kimmerle, W., Lyons, R., Sandling, R. and Teague, D. N., ‘Composition factors from the group ring and Artin’s theorem on orders of simple groups’, Proc. Lond. Math. Soc. (3) 60 (1990), 89–122.Google Scholar
Kleidman, P. B. and Liebeck, M. W., The Subgroup Structure of the Finite Classical Groups, London Mathematical Society Lecture Note Series, 129 (Cambridge University Press, Cambridge, 1990).CrossRefGoogle Scholar
Liebeck, M. W., ‘On the orders of maximal subgroups of the finite classical groups’, Proc. Lond. Math. Soc. (3) 50 (1985), 426–446.CrossRefGoogle Scholar
Liebeck, M. W. and Shalev, A., ‘Simple groups, probabilistic methods, and a conjecture of Kantor and Lubotzky’, J. Algebra 184(1) (1996), 31–57.CrossRefGoogle Scholar
Maróti, A., ‘On the orders of primitive groups’, J. Algebra 258(2) (2002), 631–640.CrossRefGoogle Scholar
Menezes, N. E., ‘Random generation and chief length of finite groups’, PhD Thesis, University of St Andrews, 2013.Google Scholar
Menezes, N. E., Quick, M. and Roney-Dougal, C. M., ‘The probability of generating a finite simple group’, Israel J. Math. 198(1) (2013), 371–392.CrossRefGoogle Scholar
Piccard, S., ‘Sur les bases du groupe symétrique et du groupe alternant’, Math. Ann. 116(1) (1939), 752–767.CrossRefGoogle Scholar
Taylor, D. E., The Geometry of the Classical Groups (Heldermann, Berlin, 1992).Google Scholar