Hostname: page-component-78c5997874-t5tsf Total loading time: 0 Render date: 2024-11-13T09:17:56.692Z Has data issue: false hasContentIssue false
  • English
  • Français

On the L1-convergence of Fourier transforms

Part of: Harmonic analysis in one variable Real functions

Published online by Cambridge University Press:  09 April 2009

Dᾰng Vũ Giang  and
Ferenc Móricz
Dᾰng Vũ Giang
Affiliation:
Institute of Mathematics University of Veszprém Egyetemu. 10. 8201 Veszprém, Hungary
Ferenc Móricz
Affiliation:
Bolyai Institute University of Szeged Aradivértanúk tere 1 6720 Szeged, Hungary
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We study cosine and sine Fourier transforms defined by F(t):= (2/π) 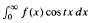and 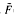(t):= (2/π), 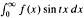where f is L1-integrable over[0, ∞]. We also assume than F 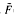are locally absolutely continuous over [0, ∞). In particular, this is the case if both f(x) and xf(x) are (L1-integrable over [0, ∞). Motivated by the inversion formulas, we consider the partial integras Sν (f, x):= 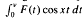and 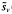ν(f, x):= 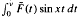, the modified partial integrals uν (f, x):= sν(f, x) - F(ν)(sin νx)/x and ũν(f, x):= 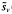ν(f, x) + 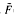(ν) (cos νx)/x, where ν > 0. We give necessary and sufficient conditions for(L1 [0, ∞)-convergence of uν (f) and ũν (f) as well as for the L1 [0, X]-convergence of sν (f) and 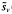ν(f) to f as ν← ∞, where 0 < X < ∞ is fixed. On the other hand, in certain cases we conclude that sν(f) and 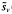ν(f) cannot belong to (L1 [0,∞). Conequently, it makes no sense to speak of their (L1 [0, ∞)-convergence as ν ← ∞.

As an intermediate tool, we use the Cesàro means of Fourier transforms. Then we prove Tauberian type results and apply Sidon type inequalities in order to obtain Tauberian conditions of Hardy-Karamata kind.

We extend these results to the complex Fourier transform defined by G(t):= 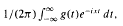, where g is L1- integrable over (−∞, ∞).

Keywords

consine and sine Fourier transformscomplex Fourier transformabsolute continutiyL1-convergenceinversion formulapartial integralCesàro meanmodified partial integralTauberian condition of Hardy-Karamata kindSidon type inequalities.

MSC classification

Secondary: 42A38: Fourier and Fourier-Stieltjes transforms and other transforms of Fourier type 26A46: Absolutely continuous functions
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 60 , Issue 3 , June 1996 , pp. 405 - 420
Copyright
Copyright © Australian Mathematical Society 1996

References

[1]Bray, W. O. and Stanojevć, Č. V., ‘Tauberian L1-convergence classes of Fourier series II’, Math. Ann. 269 (1984), 469–486.CrossRefGoogle Scholar
[2]Chen, Chang-Pao, ‘L1-convergence of Fourier series’, J. Austral. Math. Soc. (Series A) 41 (1986), 376–390.CrossRefGoogle Scholar
[3]Giang, Dᾰng Vũ and Móricz, F., ‘Lebesgue integrability of Fourier transforms’, Acta. Sci. Math. (Szeged) 60 (1995), 329–343.Google Scholar
[4]Stanojević, Č. V., ‘Structure of Fourier and Fourier-Stieltjes coefficients of series with slowly varying convergence moduli’, Bull. Amer. Math. Soc. New Ser. 19 (1988), 283–286.Google Scholar
[5]Titchmarsh, E. C., Introduction to the theory of Fourier integrals (Clarendon Press, Oxford, 1937).Google Scholar
[6]Zygmund, A., Trigonometric series (Cambridge University Press, Cambridge, 1959).Google Scholar