No CrossRef data available.
Article contents
On The Maximum of the Geometric Moving Average
Published online by Cambridge University Press: 09 April 2009
Extract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
By the geometric moving average of the independent, identically distributed random variables {Xn}, we mean the stochastic process 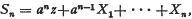 , where a is a real number such that 0≦a≦1.
, where a is a real number such that 0≦a≦1.
Information
- Type
- Research Article
- Information
- Journal of the Australian Mathematical Society , Volume 9 , Issue 1-2 , February 1969 , pp. 100 - 108
- Copyright
- Copyright © Australian Mathematical Society 1969
References
[1]Feller, W., An introduction to probability theory and its applications (Vol. II., Wiley & Sons, New York, 1966).Google Scholar
[2]Gumbel, E. J., Statistics of extremes (Columbia University Press, New York, 1958).CrossRefGoogle Scholar
[3]Kemperman, J. H. B., The passage problem for a stationary Markov chain (University of Chicago Press, 1961).CrossRefGoogle Scholar

