Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-25T17:15:57.642Z Has data issue: false hasContentIssue false
  • English
  • Français

ON THE NUMBER OF SUBSEMIGROUPS OF DIRECT PRODUCTS INVOLVING THE FREE MONOGENIC SEMIGROUP

Part of: Semigroups

Published online by Cambridge University Press:  01 February 2019

ASHLEY CLAYTON Open the ORCID record for ASHLEY CLAYTON [Opens in a new window]  and
NIK RUŠKUC Open the ORCID record for NIK RUŠKUC [Opens in a new window]
ASHLEY CLAYTON
Affiliation:
School of Mathematics and Statistics, University of St Andrews, St Andrews, KY16 9SS, UK email ac323@st-andrews.ac.uk
NIK RUŠKUC*
Affiliation:
School of Mathematics and Statistics, University of St Andrews, St Andrews, KY16 9SS, UK email nik.ruskuc@st-andrews.ac.uk
*
✉nik.ruskuc@st-andrews.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

The direct product 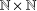$\mathbb{N}\times \mathbb{N}$ of two free monogenic semigroups contains uncountably many pairwise nonisomorphic subdirect products. Furthermore, the following hold for 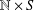$\mathbb{N}\times S$, where $S$ is a finite semigroup. It contains only countably many pairwise nonisomorphic subsemigroups if and only if 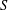$S$ is a union of groups. And it contains only countably many pairwise nonisomorphic subdirect products if and only if every element of 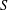$S$ has a relative left or right identity element.

Keywords

subdirect productsubsemigroupfree monogenic semigroup

MSC classification

Primary: 20M99: None of the above, but in this section
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 109 , Issue 1 , August 2020 , pp. 24 - 35
Check for updates
Copyright
© 2019 Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Baumslag, G. and Roseblade, J. E., ‘Subgroups of direct products of free groups’, J. Lond. Math. Soc. 30 (1984), 44–52.Google Scholar
Bridson, M. R., Howie, J., Miller, C. F. III and Short, H., ‘Subgroups of direct products of limit groups’, Ann. of Math. (2) 170 (2009), 1447–1467.Google Scholar
Bridson, M. R., Howie, J., Miller, C. F. III and Short, H., ‘On the finite presentation of subdirect products and the nature of residually free groups’, Amer. J. Math. 135 (2013), 891–933.Google Scholar
Bridson, M. R. and Miller, C. F. III, ‘Structure and finiteness properties of subdirect products of groups’, Proc. Lond. Math. Soc. 98 (2009), 631–651.Google Scholar
Grillet, P. A., Commutative Semigroups (Kluwer, Dordrecht, 2001).Google Scholar
Grunewald, F. J., ‘On some groups which cannot be finitely presented’, J. Lond. Math. Soc. 17 (1978), 427–436.Google Scholar
Howie, J. M., Fundamentals of Semigroup Theory, LMS Monographs, 12 (The Clarendon Press, New York, 1995).Google Scholar
Mayr, P. and Ruškuc, N., ‘Generating subdirect products’, Preprint, 2018, arXiv:1802.09325.Google Scholar
Mihaĭlova, K. A., ‘The occurrence problem for direct products of groups’, Mat. Sb. (N.S.) 70 (1966), 241–251.Google Scholar
Sit, W. and Siu, M.-K., ‘On the subsemigroups of ℕ’, Math. Mag. 48 (1975), 225–227.Google Scholar