Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-26T03:59:40.155Z Has data issue: false hasContentIssue false
  • English
  • Français

ON THE RANK OF A VERBAL SUBGROUP OF A FINITE GROUP

Part of: Special aspects of infinite or finite groups Representation theory of groups

Published online by Cambridge University Press:  12 May 2021

ELOISA DETOMI ,
MARTA MORIGI Open the ORCID record for MARTA MORIGI [Opens in a new window]  and
PAVEL SHUMYATSKY
ELOISA DETOMI
Affiliation:
Dipartimento di Ingegneria dell’Informazione, Università di Padova, Via G. Gradenigo 6/B, 35121Padova, Italy e-mail: eloisa.detomi@unipd.it
MARTA MORIGI*
Affiliation:
Dipartimento di Matematica, Università di Bologna, Piazza di Porta San Donato 5, 40126Bologna, Italy
PAVEL SHUMYATSKY
Affiliation:
Department of Mathematics, University of Brasilia, Brasilia-DF, 70910-900, Brazil e-mail: pavel@unb.br
*
e-mail: marta.morigi@unibo.it
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We show that if w is a multilinear commutator word and G a finite group in which every metanilpotent subgroup generated by w-values is of rank at most r, then the rank of the verbal subgroup 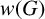$w(G)$ is bounded in terms of r and w only. In the case where G is soluble, we obtain a better result: if G is a finite soluble group in which every nilpotent subgroup generated by w-values is of rank at most r, then the rank of 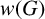$w(G)$ is at most $r+1$ .

Keywords

multilinear commutator wordsrankverbal subgroup

MSC classification

Primary: 20D20: Sylow subgroups, Sylow properties, $pi$-groups, $pi$-structure
Secondary: 20F12: Commutator calculus
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 113 , Issue 2 , October 2022 , pp. 145 - 159
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (https://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s), 2021. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Footnotes

Communicated by Ben Martin

The first and second authors are members of GNSAGA (Indam). The third author was partially supported by FAPDF and CNPq.

References

Acciarri, C., Fernàndez-Alcober, G. A. and Shumyatsky, P., ‘A focal subgroup theorem for outer commutator words’, J. Group Theory 15 (2012), 397–405.CrossRefGoogle Scholar
da Silva Alves, J. and Shumyatsky, P., ‘On nilpotency of higher commutator subgroups of a finite soluble group’, Arch. Math., 116 (2021), 1–6.CrossRefGoogle Scholar
Detomi, E., Morigi, M. and Shumyatsky, P., ‘Bounding the exponent of a verbal subgroup’, Ann. Mat. Pura Appl. (4) 193 (2014), 1431–1441.CrossRefGoogle Scholar
Detomi, E., Morigi, M. and Shumyatsky, P., ‘On countable coverings of word values in profinite groups’, J. Pure Appl. Algebra 219 (2015), 1020–1030.CrossRefGoogle Scholar
Detomi, E., Morigi, M. and Shumyatsky, P., ‘Profinite groups with restricted centralizers of commutators’, Proc. Roy. Soc. Edinburgh Sect. A 150 (2020), 2301–2321.CrossRefGoogle Scholar
Detomi, E. and Shumyatsky, P., ‘On the length of a finite group and of its 2-generator subgroups’, Bull. Braz. Math. Soc. (N.S.) 47 (2016), 845–852.CrossRefGoogle Scholar
Dixon, J. D., The Structure of Linear Groups (Van Nostrand Reinhold Company, London, 1971).Google Scholar
Fernández-Alcober, G. A. and Morigi, M., ‘Outer commutator words are uniformly concise’, J. Lond. Math. Soc. (2) 82 (2010), 581–595.CrossRefGoogle Scholar
Gorenstein, D., Finite Groups (Chelsea Publishing Company, New York, 1980).Google Scholar
Gorenstein, D., Finite Simple Groups: An Introduction to Their Classification (Plenum Press, New York, 1982).CrossRefGoogle Scholar
Guralnick, R., ‘On the number of generators of a finite group’, Arch. Math. 53 (1989), 521–523.CrossRefGoogle Scholar
Khukhro, E. I. and Shumyatsky, P., ‘Nonsoluble and non- $p$ -soluble length of finite groups’, Israel J. Math. 207 (2015), 507–525.CrossRefGoogle Scholar
Kurdachenko, L. A. and Shumyatsky, P., ‘The ranks of central factor and commutator groups’, Math. Proc. Cambridge Philos. Soc. 154 (2013), 63–69.CrossRefGoogle Scholar
Liebeck, M. W., O’Brien, E. A., Shalev, A. and Tiep, P. H., ‘The Ore conjecture’, J. Eur. Math. Soc. 12(4) (2010), 939–1008.CrossRefGoogle Scholar
Longobardi, P. and Maj, M., ‘On the number of generators of a finite group’, Arch. Math. (Basel) 50 (1988), 110–112.CrossRefGoogle Scholar
Lubotzky, A. and Mann, A., ‘Powerful p-groups. I. Finite groups’, J. Algebra 105 (1987), 484–505.CrossRefGoogle Scholar
Lucchini, A., ‘A bound on the number of generators of a finite group’, Arch. Math. 53 (1989), 313–317.CrossRefGoogle Scholar
Robinson, D. J. S., A Course in the Theory of Groups , 2nd edn, Graduate Texts in Mathematics, 80 (Springer-Verlag, New York, 1996).CrossRefGoogle Scholar
Segal, D., Words: Notes on Verbal Width in Groups , London Mathematical Society Lecture Note Series, 361 (Cambridge University Press, Cambridge, 2009).CrossRefGoogle Scholar
Shumyatsky, P., ‘On the exponent of a verbal subgroup in a finite group’, J. Aust. Math. Soc. 93 (2012), 325–332.CrossRefGoogle Scholar
Turner-Smith, R. F., ‘Marginal subgroup properties for outer commutator words’, Proc. Lond. Math. Soc. (3) 14 (1964), 321–341.CrossRefGoogle Scholar